Inscribed and Circumscribed Circles and Polygons

A series of five articles on circles.

1) Introduction to Circles

2) Geometry: Circles and Angles

3) Circle and Line diagrams

4) Inscribed and Circumscribed Circles and Polygons

5) Slicing up Circles: Arclengths, Sectors, and Pi

Inscribed and circumscribed

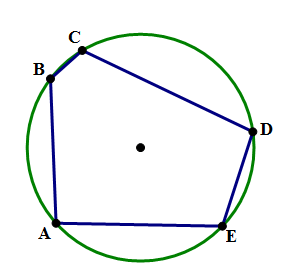
One more sophisticated type of geometric diagram involves polygons “inside” circles or circles “inside” polygons. When a polygon is “inside” a circle, every vertex must lie on the circle:

In this diagram, the irregular \space pentagon \space ABCDE is inscribed in the circle, and the circle is circumscribed around the pentagon. We can also say: the circle circumscribes the pentagon. The word “inscribed” describes the inside shape, and the word “circumscribed” describes the outside shape. Here's another diagram with the polygon on the outside.

Notice, now, that each side of this irregular pentagon is tangent to the circle. Now, the pentagon is circumscribed around the circle, and the circle is inscribed in the pentagon. In both cases, the outer shape circumscribes, and the inner shape is inscribed.

Triangles

As is the case repeatedly in discussions of polygons, triangles are a special case in the discussion of inscribed & circumscribed. Every single possible triangle can both be inscribed in one circle and circumscribe another circle. That “universal dual membership” is true for no other higher order polygons —– it's only true for triangles. Here's a small gallery of triangles, each one both inscribed in one circle and circumscribing another circle.

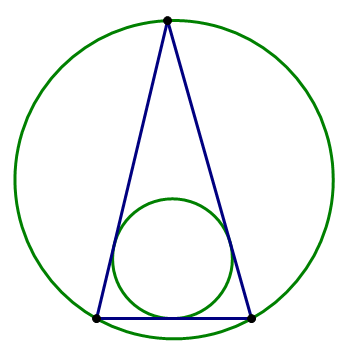
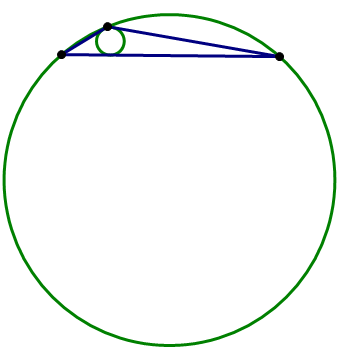
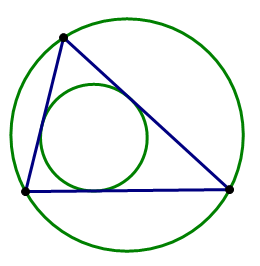
Notice that, when one angle is particularly obtuse, close to 180\degree, the size difference between the circumscribe circle and the inscribed circle becomes quite large. Notice, also: in the case of a right triangle, the second image, the hypotenuse of the triangle is the diameter of the circumscribed circle. We will return to this point.

Quadrilaterals

Many quadrilaterals can be neither inscribed in a circle nor circumscribed by a circle: that is it say, it is impossible to construct a circle that passes through all four vertices, and it is also impossible to construct a circle to which all four sides are tangent.

Some quadrilaterals, like an oblong rectangle, can be inscribed in a circle, but cannot circumscribe a circle. Other quadrilaterals, like a slanted rhombus, circumscribe a circle, but cannot be inscribed in a circle.

An elite few quadrilaterals can both circumscribe one circle and be inscribed in another circle. Of course, the square (below, left), the most elite of all quadrilaterals, has this property. Another example is the “right kite” (below, right), a kite with a pair of opposite right angles:

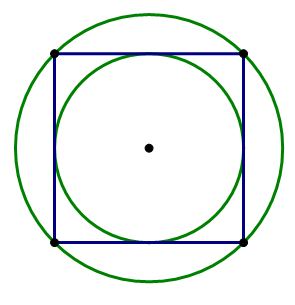
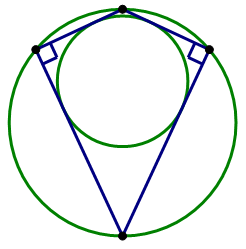
While this “dual membership” is true for all triangles, it's limited to some special cases with quadrilaterals.

Higher Polygons

What was true for quadrilaterals is also true for all higher polygons.

• Most, the vast majority, can neither circumscribe a circle nor be inscribed a circle.
• Some can be inscribed in a circle, but cannot circumscribe a circle.
• Some can circumscribe a circle, but cannot be inscribed in a circle.
• An elite few can both circumscribe a circle and be inscribed in a circle.

That last category, the elite members, always includes the regular polygon. Just as all triangles have this “dual membership”, so do all regular polygons. Here's a gallery of regular polygons, with both their inscribed circle and their circumscribing circle.

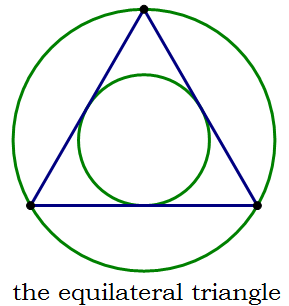
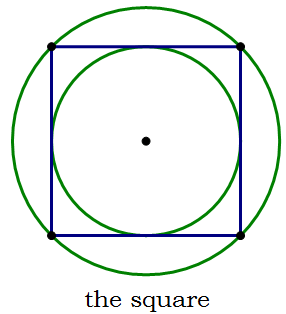
Obviously, as the number of sides increases, the sizes of the two circles become closer and closer.

QUANT questions about inscribed and circumscribed polygons are rare, and may test both your understanding of terminology and your visualization skills by describing the geometric situation (e.g. “rectangle JKLM is inscribed in a circle”) and not giving you a diagram.

A special case: a triangle inscribed in a semicircle

This is one special case the QUANT loves. It could easily appear somewhere on the Quant section of your real QUANT.

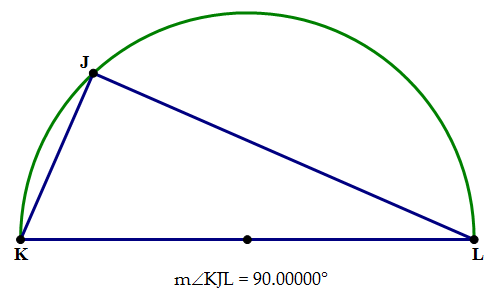
If all you know is that KL is the diameter of the circle, that's sufficient to establish that \angle{J} = 90\degree and that \triangle{JKL} is a right triangle with KL as the hypotenuse. Alternately, if all you know is that \triangle{JKL} is a right triangle with KL as the hypotenuse, that's sufficient to establish that arc KJL is a semicircle and KL is a diameter. This is a powerful set of ideas because the deductions run both ways and because it inextricably connects two seemingly disparate ideas.

Practice question

Q1. In the diagram above, S is the center of the circle. If QS = 5 and QR = 6, what is PQ?

A. 7

B. 8

C. 9

D. 10

E. 11

Practice question explanation

Q1. First of all, QS is a radius, so if QS = 5, that means PS = SR = 5 and the diameter PR = 10. Furthermore, because PR is a diameter, that means \triangle{PQR} is a right triangle, with \angle{PQR} = 90\degree. We know two sides of this right triangle: QR = 6, and PR = 10, so we can use the Pythagorean Theorem to find the third side.

(PQ)^2 + (QR)^2 = (PQ)^2

(PQ)^2 + (6)^2 = (10)^2

(PQ)^2 + 36 = 100

(PQ)^2 = 100 - 36 = 64

PQ = \sqrt{64} = 8

Answer = B