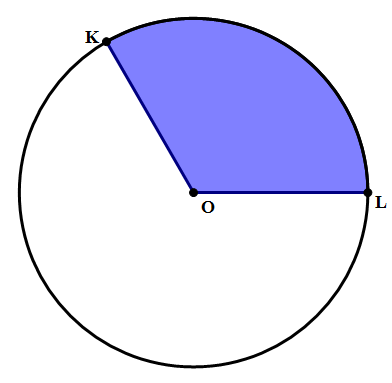Angles of a Circle

A series of five articles on circles.

Suppose you stand at the center of a circle and turn around that you face each and every point on the circle. You would turn all the way around, which is an angle of 360\degree. In this sense, a whole circle has an angle of 360\degree. If you divided a circle equally, you could calculate the angle of each “slice”. Here are a few division results that could help you to know on test day (I’m just giving the ones that come out as nice round numbers, not the ones that result in ugly decimals):

\dfrac{360}{2} = 180

\dfrac{360}{3} = 120

\dfrac{360}{4} = 90

\dfrac{360}{5} = 72

\dfrac{360}{6} = 60

\dfrac{360}{8} = 45

\dfrac{360}{9} = 40

\dfrac{360}{10} = 36

\dfrac{360}{12} = 30

Arcs and Arclength

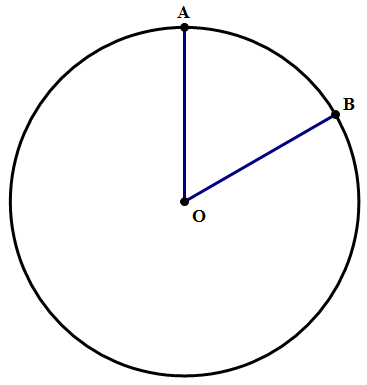
Suppose we look at a “slice” of a circle, like a slice of pizza.

The curved line from A to B, a part of the circle itself, is called an arc. This corresponds to the crust of the pizza.

We can talk about the size of an arc in one of two ways: (a) its angle, sometimes called “arc angle” or “arc measure”, and (b), its length, called arclength. The angle of the arc, its arc measure, is just the same as the angle at the center of the circle. Here \angle{AOB} = 60\degree, so the measure of arc AB is 60\degree.

We find the arclength by setting up a proportion of part-to-whole. The angle is part of the whole angle of a circle, 360\degree. The arclength is part of the length all the way around, i.e. the circumference. Therefore:

\dfrac{part}{whole} = \dfrac{angle}{360\degree} = \dfrac{arclength}{2\pi{r}}

Here, let’s say the radius is r = 12. Then, the circumference is c = 24{\pi}. Since the angle is 60\degree, the ratio on the left side, \dfrac{angle}{360}, becomes \dfrac{1}{6}. Call the arclength x.

{\dfrac{1}{6}} = {\dfrac{x}{24\pi}}

Cross-multiply:

{24{\pi}} = 6x

{4{\pi}} = x = arclength

In other words, since the angle 60\degree is one sixth of the full angle of a circle, the arclength is one sixth of the circumference.

Finally, here’s a practice question.

Practice Question

1) In the shaded region above, \angle{KOL} = 120\degree, and the area of the entire circle is A = 144{\pi}. The perimeter of the shaded region is

(A) 12 + 8{pi}

(B) 12 + 16{pi}

(D) 24 + 16{pi}

(E) 24 + 24{pi}

Practice Question Explanation

1) The area 144{\pi} = {{\pi}r^2}, so r = 12. This means KO = 12 and OL = 12, so those two sides together are 24. The remaining side is arc KL. The whole circumference is c = 2{\pi}r = 24{\pi}. The angle of 120\degree is \dfrac{1}{3} of a circle, so the arclength is \dfrac{1}{3} of the circumference. This means, arclength = 8{\pi}, and therefore the entire perimeter is 24 + 8{\pi}.

Answer = C