Slicing up Circles: Arclength, Sectors, and Pi
A series of five articles on circles.
1) Introduction to Circles
2) Geometry: Circles and Angles
3) Circle and Line diagrams
4) Inscribed and Circumscribed Circles and Polygons
5) Slicing up Circles: Arclengths, Sectors, and Pi
Few topics perplex students like circles on the QUANT. “What was the formula for area of a circle, again? I know pi is in there somewhere!” With a few simple insights, though, this entire topic simplifies. First, let’s look at a problem. How do you find the do calculations for something like this?
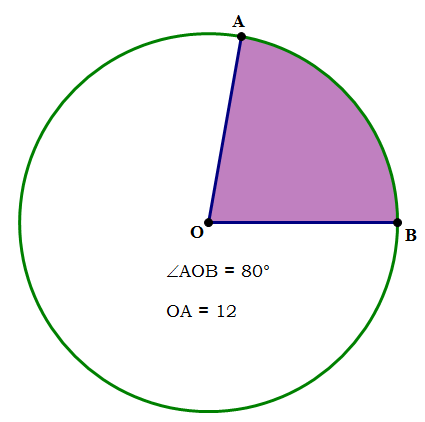
Given that O is the center of the circle, and given the info in the diagram, how do we find (1) the length of arc AB? and (2) the area of sector AOB (i.e. the shaded region)? BTW, the word sector is the name for a “slice of pie” piece of a circle, and arclength is the curved length along the “crust” of the pie. You can find a little more about arclength at this Web Page — Geometry: Circles and Angles.
Proportions
One of the greatest math “tricks” is proportional reasoning, and this is precisely what unlocks all the questions posed above. Basically, to find either the length of an arc or the area of sector, we set up a part-to-whole ratio, and set this equal to a ratio for the angle. In the diagram, the angle at the center of the circle is 80\degree. A whole circle, all the way around, is always 360\degree, so this 80\degree angle takes up \dfrac{80}{360} = \dfrac{8}{36} = \dfrac{2}{9} of a circle. Therefore, both the arclength and the area of the sector are \dfrac{2}{9} of their respective “wholes”.
Arclength
If arclength is the “part”, then the “whole” is the length all the way around the circle — we call that length circumference, and its formula is
\LARGE{c = 2\pi{r}}
The part-over-whole of the angles has to equal the part-over-whole of these lengths:
\dfrac{central \space angle}{360\degree} = \dfrac{arclength}{2\pi{r}}
For this diagram, this proportion becomes:
Area of a sector
If area of the sector is the “part”, then the area of the whole circle is the whole. Of course, for the area of a circle, we use Archimedes' remarkable formula:
\LARGE{A = \pi{r^2}}
As with arclength, the part-over-whole of the angles has to equal part-over-whole of these areas:
\dfrac{central \space angle}{360\degree} = \dfrac{area \space of \space sector}{\pi{r^2}}
For this diagram, this proportion becomes:
\dfrac{central \space angle}{360\degree} = \dfrac{area \space of \space sector}{\pi{r^2}}
\to \dfrac{2}{9} = \dfrac{area \space of \space sector}{\pi{12^2}}
\to \dfrac{2}{9} = \dfrac{area \space of \space sector}{144\pi}
\to area \space of \space sector = \dfrac{2*144\pi}{9}
\to area \space of \space sector = 2*16\pi = 32\pi
BTW, a mental math tip — how did I just know, in my head, that \dfrac{144}{9} = 16, or in other words, that 9*16 = 144? Well, think about it.
If 12=3*4, then 12^2={3^2}*{4^2} \to 144=9*16
That logic makes it very easy to find factors of perfect squares.
Practice question
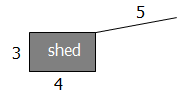
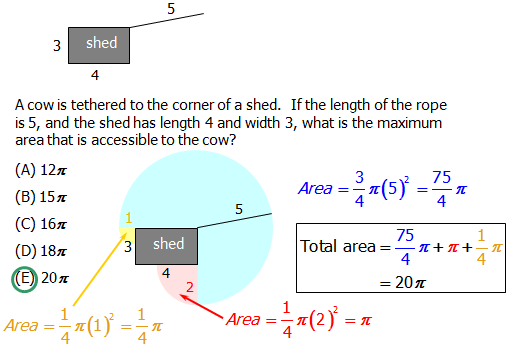
A cow is tethered to the corner of a rectangular shed. If the length of the rope is 5, and the shed has length 4 and width 3, what is the maximum area that is accessible to the cow? (The cow cannot enter the shed).
A. 12\pi
B. 15\pi
C. 16\pi
D. 18\pi
E. 20\pi
Explanation:
FAQ: How do we know the blue area is \dfrac{3}{4} of a circle, and that the yellow and red areas are \dfrac{1}{4} of a circle?
A: For the largest portion of the roaming area, we use \dfrac{3}{4} of a circle because of the information we know about the shed. The problem tells us it is rectangular, so we know that the corners of the shed are all 90\degree. The shed essentially drives a wedge into the circle from the center and takes up 90\degree or \dfrac{1}{4} of the circle's possible area, blocking roaming access. (90\degree out of a total 360\degree is \dfrac{90}{360} = \dfrac{1}{4}.)
Also, by continuation of this logic, we know we can use \dfrac{1}{4} on each of the ends because when we visualize the area of the \dfrac{3}{4} circle we just discussed above, and we consider the square corners of the shed again, we know the maximum area that rope can extend will be a 90\degree angle at each corner.
FAQ: Will a question like this actually show up on the exam?
A: You should consider all of our practice questions as possible questions on the actual test. :) They're designed specifically to mimic the difficulty level and content tested on the actual exam.