An Introduction to Circles

A series of five articles on circles.

1) Introduction to Circles

2) Geometry: Circles and Angles

3) Circle and Line diagrams

4) Inscribed and Circumscribed Circles and Polygons

5) Slicing up Circles: Arclengths, Sectors, and Pi

Here is a rundown of geometry facts you might need to know about circles.

The Basic Terminology

A circle is the set of all points equidistant from a fixed point. That means a circle is this:

and not this:

In other words, the circle is only the curved round edge, not the middle filled-in part. A point on the edge is “on the circle”, but a point in the middle part is “in the circle” or “inside the circle.” In the diagram below,

point \space A is on the circle, but point \space B is in the circle.

By far, the most important point in the circle is the center of the circle, the point equidistance from all points on the circle.

Chords

Any line segment that has both endpoints on the circle is a chord.

By the way, the word “chord” in this geometric sense is actually related to “chord” in the musical sense: the link goes back to Mr. Pythagoras (c. 570 – c. 495 BCE), who was fascinated with the mathematics of musical harmony.

If the chord passes through the center, this chord is called a diameter. The diameter is a chord. A diameter is the longest possible chord. A diameter is the only chord that includes the center of the circle.

The diameter is an important length associated with a circle, because it tells you the maximum length across the circle in any direction.

An even more important length is the radius. A radius is any line segment with one endpoint at the center and the other on the circle.

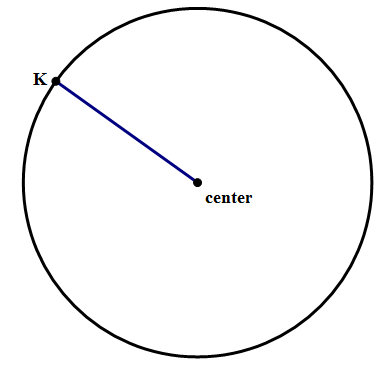
As is probably clear visually, the radius is exactly half the diameter, because a diameter can be divided into two radii. The radius is crucially important, because if you know the radius, it's easy to calculate not only the diameter, but also the other two important quantities associated with a circle: the circumference and the diameter.

Circle Formulas

The circumference is the length of the circle itself. This is a curve, so you would have to imagine cutting the circle and laying it flat against a ruler. As it turns out, there is a magical constant that relates the diameter (d) & radius (r) to the circumference. Of course, that magical constant is \pi. From the very definition of \pi itself, here are two equations for the circumference, c.

\LARGE{c = {\pi}d}

\LARGE{c = 2{\pi}r}

If you remember the second, more common form, you don't need to know the first. The number \pi is slightly larger than 3 — this means that three pieces of string, each as long as the diameter, together would not be quite long enough to make it all the way around the circle. The number \pi can be approximated by 3.14 or by the fraction \dfrac{22}{7}. Technically, it is an irrational number that goes on forever in a non-repeating pattern.

These two formulas follow from the definition of \pi, so basically every culture on earth figured out these. By contrast, the area of circle was discovered by one brilliant mathematician, and everyone on earth has this one man to thank for his formula for the area of a circle. That man was Archimedes (c. 287 – c. 212 BCE). Here is Archimedes' amazing formula:

\LARGE{A = {\pi}{r^2}}

This is another formula you need to know cold on test day.

Practice Problems

1) Given that a “\bold{12}-inch pizza” means circular pizza with a diameter of 12 inches, changing from an 8-inch pizza to a 12-inch pizza gives you approximately what percent increase in the total amount of pizza?

(A) 33

(B) 50

(C) 67

(D) 80

(E) 125

2) What is the diameter of circle Q?

Statement #1 — the circumference of Q is c = 12{\pi}.

Statement #2 — the area of Q is A = 36{\pi}.

Practice Problem Solutions

Q1. The 8-inch pizza has a radius of r = 4, so the area is A = 16{\pi}. That area is how much pizza you get. The 12-inch pizza has a radius of r = 6 and an area of A = 36{\pi}. When you change from 16 to 36, what is the percentage change? Well, that’s more than double, so it must be a percent greater than 100\%. The only answer choice greater than 100\% is answer E.

Q2. Statement #1: if you know the circumference, then you can use c = 2{\pi}r to solve for the radius, or c = {\pi}d to solve for the diameter. Either way, you can find the diameter, so this statement by itself is sufficient.

Statement #2: if you know the area, you can find the radius, and then double that to get the diameter. This statement by itself is also sufficient.

Both statements alone are sufficient.

Answer = D