The Pythagorean Theorem

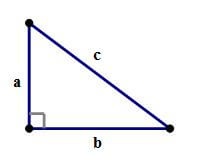
There’s a reason this is the most famous theorem in mathematics! This remarkable theorem is one of the most versatile and highly adaptable formulas in existence. Of course, I’m sure you remember that it says: For any right triangle,

\bold{a^2 + b^2 = c^2}

Of course, if any question gives you two sides of a right triangle and asks you to find the third, you will use this formula. Here are a couple problems to show its other guises.

Practice Questions: Using the Pythagorean Theorem

Q1. In the coordinate plane, point \space A has coordinates (-2, -1) and point \space B has coordinates (4, 7). What is the length of segment AB?

(A) 10

(B) 10.5

(C) 12

(D) 13.675

(E) 14

Q2. Paul drove 50 miles north, then changed direction and drove 120 miles east. At the end of this trip, how far was he from his starting point?

(A) 70 miles

(B) 110 miles

(C) 130 miles

(D) 150 miles

(E) 170 miles

Answers and Explanations

Q1. The easiest distances to find in the coordinate plane are the horizontal and vertical lines, so we begin by drawing those.

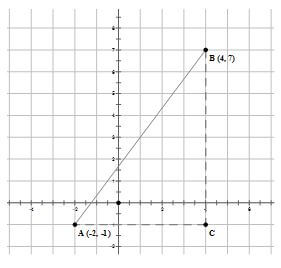
For the lengths of AC and BC, we can simply count boxes. AC = 6 and BC = 8. These are the two “legs” of a right triangle, and AB is the hypotenuse, so

(AC)^2+(BC)^2=(AB)^2

(6)^2+(8)^2=(AB)^2

36+64=100=(AB)^2

AB=10

Answer = A

Q2. Essentially, Paul drove along the legs of a big right triangle, and the hypotenuse is how far he is from his starting point.

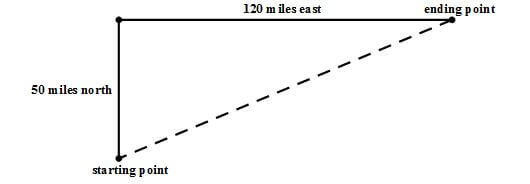
Therefore,

(distance \space from \space start)^2

=50^2+120^2

=2500+14400

=16900\todistance \space from \space start

=\sqrt{16900}=130

Answer = C