Geometric Probability

In the first three articles in this series on QUANT probability questions, I discussed the AND and OR probability rules, "at least" probability questions, and probability questions that involve counting. This post covers relatively rare kind of probability question not covered in the first three posts: geometric probability questions. First, a few challenging practice QUANT questions on this topic.

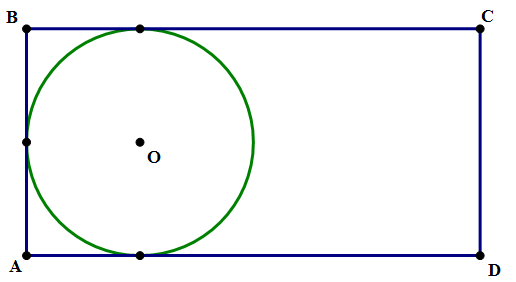
1. In the diagram above, the sides of rectangle $ABCD$ have a ratio $AB:BC = 1:2$, and the circle is tangent to three sides of the rectangle. If a point is chosen at random inside the rectangle, what is the probability that it is not inside the circle?

A. $\dfrac{4-\pi}{4}$

B. $\dfrac{4+\pi}{4}$

C. $\dfrac{4+\pi}{8}$

D. $\dfrac{8-\pi}{8}$

D. $\dfrac{8+\pi}{8}$

2. Region $R$ is a square in the $x$-$y$ plane with vertices $J = (-1, -2)$, $K = (-1, 4)$, $L = (5, 4)$, and $M = (5, -2)$. What is the probability that a randomly selected point in region $R$ lies below the line $3x - 5y = 10$?

A. $\dfrac{5}{12}$

B. $\dfrac{5}{18}$

C. $\dfrac{5}{24}$

D. $\dfrac{5}{36}$

E. $\dfrac{5}{72}$

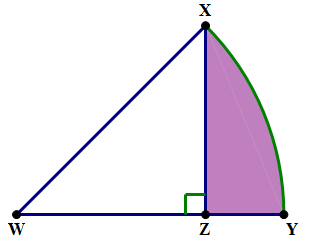
3. In the diagram above, $WZ = XZ$, and circular arc $XY$ has a center at $W$. If a point is selected from anywhere within this figure, what is the probability that it is selected from the shaded region?

A. $\dfrac{\pi-2}{\pi}$

B. $\dfrac{\pi-1}{2\pi}$

C. $\dfrac{2\pi-3}{4\pi}$

D. $\dfrac{4\pi-1}{8\pi}$

E. $\dfrac{6\pi-3}{8\pi}$

4. If points $A$ and $B$ are randomly placed on the circumference of a circle with radius $2$, what is the probability that the length of chord $AB$ is greater than $2$?

A. $\dfrac{1}{4}$

B. $\dfrac{1}{3}$

C. $\dfrac{1}{2}$

D. $\dfrac{2}{3}$

E. $\dfrac{3}{4}$

These three are very challenging problems. If they seem easy to you, you are probably a QUANT Quantitative expert! If these make your head spin, please read on!

Probability and area

As anti-intuitive as this may seem, there is a deep mathematical link between probability and area. For example, if you are dealing with regions under the Normal Distribution or any other distribution, the probability of landing in those regions is measured by finding the area under the curve. This connection between area and probability because quite apparent if you happen to study calculus-based statistics. If you haven’t ventured into such regions, I’ll just say, remember: there’s an important link between probability and area. In particular, if a diagram is given or described in a Quantitative question, and you are asked for a probability, then you almost always will be finding a ratio of two areas. Thus, any geometric probability problem just becomes a 2-in1 find-the-area problem.

Finding area

Know your basic geometry. You should know how to find the area of rectangles and triangles: if you don’t remember, say, the formula for the area of a trapezoid, just break it into triangles & rectangles and find the area piece-by-piece. You should know Archimedes' remarkable formula for the area of a circle:

$A=\pi{r^2}$

You should also be comfortable with setting up the proportion necessary to find the area of a circular sector (i.e. a "slice of the pie").

Visualize

If you are given a diagram as part of the problem, that’s great. If you are not given a diagram, sketch one on the notepad. In any problem involving Geometry, it’s very important to have your right-brain visual skills engaged.

A ratio of areas

The most general formula for probability is

$probability=\dfrac{\text{number of desired coucomes}}{\text{total number of possible outcomes}}$

In the case of geometry probability, each of these terms, the numerator and the denominator, is an area.

$probability=\dfrac{\text{area of desired region}}{\text{total area}}$

Many times in geometric probability problems, as in #1 and #3 above, no absolute lengths are given — we know the relative ratios, but we don’t know in absolute terms how big anything is. The information in the problem does not allow us to compute the numerical value of any area. That’s fine. Just pick any convenient number for one of the lengths, and figure out everything from there. It doesn’t matter what value you pick, because in the probability ratio, the value you pick will cancel. All that matters are the ratios.

Summary

With these recommendations, go back and look at those problems again before reading the explanations below.

Practice question explanations

1. We aren’t given any absolute lengths. For convenience, I am going to assume that the radius of the circle is $r = 1$. That’s very easy. Right away, we know the area of the circle is $\pi$. Notice, the height of the triangle is equal to the diameter of the circle, so $h = AB = 2$. We are told the ratio of $AB:BC = 1:2$, so $BC$, the width, must equal $w = BC = 4$. Area of the rectangle is $h*w = (AB)*(BC) = 8$. That, right there, is our "denominator area". Now, for the numerator area, the area of the rectangle that does not include the circle, subtract the circle from the rectangle: $A = 8 - \pi$. That’s our numerator.

$Probability=\dfrac{8-\pi}{8}$

Answer = D

2. Here, we are not given a diagram, so we will sketch one. In the real test, just a rough diagram will be enough to visualize things. Here’s an accurate diagram.

Notice the square $JKLM$ has an area of $6 \times 6 = 36$ — right there, that’s our denominator-area.

Now, let’s think about this line. Let’s solve for $y$, to put the line into slope-intercept form (i.e. $y = mx + b$ form).

$3x-5y=10$

$3x=5y+10$

$5y=3x-10$

$y=\dfrac{3}{5}x-2$

First of all, putting it in slope-intercept form makes clear — the $y$intercept of this line is point $S$, $(0, -2)$, which is on one side of the square. The slope is $\dfrac{3}{5}$, so over five and up three puts us at point $T, (5, 1)$, also on a side of the square. Triangle $STM$ has a base of $5$ and height of three, so the area is

$A=\dfrac{1}{2}bh=\dfrac{1}{2}(5)(3)=\dfrac{15}{2}$

That’s the numerator-area, so just divide

$probability$$=\dfrac{15/2}{36}$$=\dfrac{15}{2*36}$$=\dfrac{15}{72}$$=\dfrac{5}{24}$

Answer = C

3. Again, we are not given any absolute lengths, so we will pick something convenient. Here, I am going to pick $WZ = XZ = 1$. Triangle $WXZ$ is an Isosceles Right Triangle, i.e. a $45-45-90$ triangle. Its area is $A=(\dfrac{1}{2})bh$, and since both base and height are $1$, the area of the triangle is $\dfrac{1}{2}$.

Both $WX$ and $WY$ are radii of the circle. From the proportions in the $45-45-90$ triangle, we know

$r=WX=WY=\sqrt{2}$

Now, we can find the area of the circle, using Archimedes’ formula:

$A={\pi}r^2={\pi{\bigg(\sqrt{2}\bigg)}^2}$$=2\pi$

Because triangle $WXZ$ is a $45-45-90$ triangle, we know $\angle{W} = 45\degree$. Well, a $45\degree$ angle must be half of $90\degree$ — which means a $45\degree$ is $\dfrac{1}{4}$ of $180\degree$ — which means a $45\degree$ is $\dfrac{1}{8}$ of $360\degree$. Thus, a $45\degree$ sector would be $\dfrac{1}{8}$ of a circle and have $\dfrac{1}{8}$ of the entire circle’s area.

$\it{\text{Area of sector WXY}}$$=\dfrac{\it{\text{area of circle}}}{8}$$=\dfrac{2\pi}{8}$$=\dfrac{\pi}{4}$

First of all, that’s the denominator-area in our probability. Also, we can use this to figure out the area of the shaded region.

$\it{\text{Area of shaded region}}$$=(\it{\text{area of sector}}) - (\it{\text{area of triangle}})$

$=\dfrac{\pi}{4}-\dfrac{1}{2}$

That’s our numerator-area. Now, we can put together the probability — we will just have to simply the complex fraction by multiplying numerator and denominator by $4$.

$probability$$=\dfrac{{\dfrac{\pi}{4}}-{\dfrac{1}{2}}}{\dfrac{\pi}{4}}$$=\dfrac{{\pi}-2}{\pi}$

Answer = A

4. First of all, the circle has what is called rotational symmetry, and we will take advantage of this. Because of rotational symmetry, we can pick, at random, any location we want for point $A$, and just consider how far away randomly chosen point $B$ locations would be. If the locations of points $A$ & $B$ that are, say, $3$ cm apart, it will not make any difference to the problem where $A$ and $B$ are individually on the circle — the only thing that matters to the problem is the distance between them. That's why we can simply select an arbitration location for point $A$ and consider only the random possibilities for the location of point $B$.

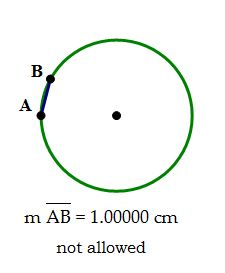
Because we are interested in an inequality (chord $\gt 2$ cm), we will employ a standard mathematical strategy of solving the equation first (chord $= 2$ cm). Even though this particular chord would not satisfy the condition, this chord or location on the circle will form, as it were, a "boundary" between the "allowed" region and the "not allowed" region. Again, this is a standard mathematic strategy, often used in algebraic inequalities for example: turn it into an equation and solve the equation first — the solutions to the equation form what mathematicians call the "boundary conditions" for the solution to the inequality.

Also, keep in mind — because point B could be randomly located anywhere on the circle, it could be on either side of point $A$ — clockwise from point $A$, or counterclockwise from point $A$. Therefore, we have to consider the (chord $= 2$) case on both sides of the circle.

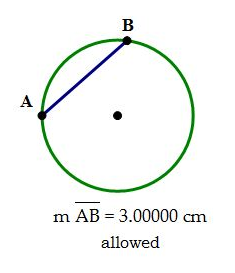
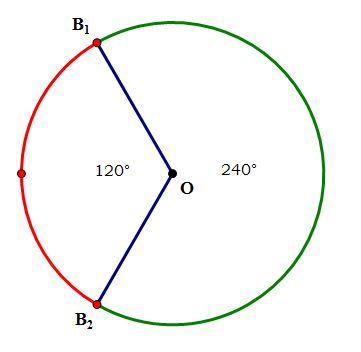
In that diagram, chords $AB_1$ and $AB_2$ both have a length of exactly $2$ cm, so those points, and anything closer to point $A$ than those points would be a "not allowed" location, a place with a chord less than or equal to $2$ cm. This is the red region on the circle. The places where the chord would be greater than $2$ cm is the green region of the circle. The probability question really reduces to a geometric question: what percent of the whole circle is the green arc?

Notice there's a most fortuitous set of connections in that diagram. There are five segments — $AO$, $AB_1$, $AB_2$, $OB_1$, & $OB_2$ — that all have the length of $2$ cm. The segments $AB_1$ & $AB_2$, were chosen to have this length, and the other three are all radii of the circle, and we are told that the length of a radius is $2$ cm.

This means the two triangles — triangle $OAB_1$ & triangle $OAB_2$ — are both equilateral triangles. (In fact, any time you have $chord = radius$, and you connect radii to the endpoints of the chord, you will get an equilateral triangle). This means that each of angles is $60\degree$. Since angle $AOB_1 = 60\degree$ and angle $AOB_2 = 60\degree$, we know that angle $B_1OB_2 = 120\degree$. This is the central angle associated with the red arc (see the lesson on "Pieces of Pi" below).

There are $360\degree$ in a circle altogether. Since there are $120\degree$ in the angle associated with the red arc, the green arc must have an angle of $360\degree - 120\degree = 240\degree$:

If point $B$ lands anywhere on the green arc, it meets the condition (chord $\gt 2$ cm), and if point $B$ lands anywhere on the red arc, it fails to meet the condition (chord $\leqslant 2$ cm). The green arc takes up $240\degree$ of the full $360\degree$ of the circle.

$Probability$$= \dfrac{240}{360}$ $= \dfrac{24}{36}$ $= \dfrac{2}{3}$

​

Answer = D