How to Solve Two Equations with Two Variables

Fact: If you have two variables and only one equation, in general you will not be able to solve for the individual values of the variables. You need two separate equations in order to solve for the individual values of each of two variables. (This fact is crucially important on the Quantitative Section.)

More Advanced Fact: As a general rule, if you wish to solve for the values of n different variables, you need at least n different equations. (If n = 3, this could possibly come into play on 168+ questions on Quantitative.)

A Boon for Data Sufficiency!

Just this one mathematical fact, the first one, has powerful implications for hundreds of possible DS questions. Consider this template DS question:

Q1. In blah blah blah scenario, x is blah blah blah and y is blah blah blah.

Statement #1: 2x + y = 6

Statement #2: x - y = 6

Statement #1: two variables, one equation, not sufficient by itself.

Statement #2: two variables, one equation, not sufficient by itself.

Combined: two equations, two variables, can be solved, sufficient.

Done.

Answer = C

Notice, we had to do a minimum of math to solve this question. Just this one fact can make short work of any of a number of seeming complicated DS questions. Often, notice that the “equations” are given in verbal form: one first has to translate, but once you realize the verbal information constitutes an equation, you don’t even need to find the question: you can just use this logic to power through to an answer.

Strategy for Problem Solving

Your Algebra Two teacher probably taught you two different ways to solve these equations. For simplicity, I am just going to review one method, the one that is most useful in solving the systems of equations you will see on the QUANT. If you remember the other method, and prefer that, by all means use it.

The method I am going to review is sometimes called “elimination” or “linear combination.” Here is the strategy.

Step #1 — Multiply one or both equations so that the coefficients of the same variable are opposites of each other (e.g. +7 and -7).

Step #2 — Add the two equations

Sometimes you get very lucky because in the equation, as given, coefficients of one variable already are opposites, so you can bypass Step #1 and proceed immediately to Step #2.

I’ll demonstrate with the two equations in my hypothetical question above. Suppose, in a PS question we were given those two equations (2x + y = 6 and x - y = 6) and had to solve for either x or y. Here, we are very lucky — the coefficients of y are opposites, all we have to do is add the two equations:

Once we know x = 4, we can plug into either equation to find that y = -2.

A Slightly More Challenging Example

Consider this question:

Q2. The symphony sells two kinds of tickets: orchestra, for \${40}, and upper tiers, for \${25}. On a certain night, the symphony sells 90 tickets and gets \${2625} in revenue from the sales. How many orchestra tickets did they sell?

(A) 25

(B) 35

(C) 45

(D) 55

(E) 65

Notice, in verbal form, this is a two-equations-two variables problem. The two variables are

x = the \space number \space of \space orchestra \space tickets,

and

y = the \space number \space of \space upper \space tier \space tickets.

One equation we get is x + y = 90, for the total number of tickets sold. That’s one equation. If we sell x orchestra tickets, we get \${40} for each, so we get 40x in total revenue from all of the orchestra tickets. Similarly, we get 25y in total revenue from all the upper tier tickets. Thus, the total revenue is 40x + 25y = 2625. That’s our second equation.

The first equation is incredibly convenient to multiply. I would rather multiply by 40 than by 25, so I make the coefficients of x match. I’ll multiply the first equation by 40, and the second equation by -1.

Now, at first blush, that might look like an ugly division problem awaiting us, 975 divided by 15. Let’s break it down a bit. I know \dfrac{900}{3} = 300, and \dfrac{75}{3} = 25, so if I divide both sides by 3, I get

5y = \dfrac{975}{3} = 325

Now, \dfrac{100}{5} = 20, so three times that is \dfrac{300}{5} = 60. Of course, \dfrac{25}{5} = 5, so

y = \dfrac{325}{5} = 65

We want x, so x + (65) = 90 right x = 25

Answer = A

BTW, if these steps totally elude you, remember you can always backsolve from the numerical answers as a backup strategy.

Practice Question

Q3. If 4x - 3y = 13 and 5x + 2y = -1, then x =

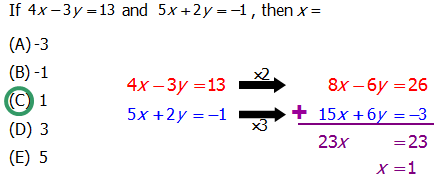
Answer = C