Backsolving on Math

Q1. What is the smallest positive integer x for which x^3 + 5x has value more than 80?

(A) 2

(B) 3

(C) 4

(D) 5

(E) 6

Q2. In the month of August, Pentheus Corporation made \${200,000} in profit. Pentheus made 6\% of that profit on the second Wednesday of August. If the profits that day were approximately 14.5\% of the revenue for that day, then what was Pentheus’s revenue on the second Wednesday of August?

(A) \${65,536}

(B) \${75,025}

(C) \${77,922}

(D) \${80,000}

(E) \${82,756}

Q3. Harold needs to buy a ticket to attend a conference for work. His own department contributes \${4} less than half the price of the ticket. The HR department will contributes \${1} more than a third of the price of the ticket. With these two contributions, Harold has to pay only \${10} out of his own pocket to cover the cost of the ticket. What was the price of the ticket?

(A) \${36}

(B) \${42}

(C) \${48}

(D) \${54}

(E) \${60}

Q4. Jackson invested \${300,000}, dividing it all unequally between Account P and Account Q. At the end of the year, it turned out that Account P had earned 12\% interest and Account Q had earned 25\% interest. If Jackson earned a total of \${60,000} in interest between the two accounts, which of the following is approximately the amount he put in account P?

(A) \${115,384}

(B) \${120,000}

(C) \${121,072}

(D) \${124,129}

(E) \${130,000}

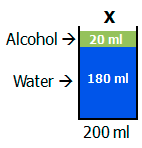
Q5. Solution X is 10 percent alcohol by volume, and solution Y is 30 percent alcohol by volume. How many milliliters of solution Y must be added to 200 milliliters of solution X to create a solution that is 25 percent alcohol by volume?

(A) \dfrac{250}{3}

(B) \dfrac{500}{3}

(C) 400

(D) 480

(E) 600

Solutions will come at the end of this article.

Backsolving basics

When all five answers are numerical, that puts us in an excellent position to use backsolving. Backsolving is an alternative to the algebraic method of solution that your wizened Algebra Two teacher would have deemed the only correct way. Backsolving means starting with a numerical answer, and working through with that number to see if it fits the requirements of the scenario.

In a previous post, I recommended the #1 backsolving strategy: start with answer (C). You see, if all five answer are integers, the QUANT always lists them from smallest to largest. Answer choice (C) will always be in the middle. If we plug in (C) and it comes out to the correct value, then we are done. If it is too big, then we can eliminate (C) & (D) & (E); if it is too small, then we can eliminate (A) & (B) & (C). Choice (C) is often the best place to start, because whether it turns out to be too high or too low, there’s more than one answer to eliminate.

Make it easy!

Of course, backsolving is a strategy that should be used to make things easier. Suppose a problem presents a scenario, and then has these answer choices:

(A) 14,641

(B) 15,000

(C) 16,384

(D) 17,711

(E) 19,683

Well, hmmm. Whatever the calculations in the problem may be, starting with (C) doesn’t seem like it would be a whole lot of fun without a calculator. Also, notice the answers are too close together to estimate. BUT, notice that of the five answer choices, here answer choice (B) is a nice neat round number. In a way, the design of the answer choices presents (B) on a silver platter as the best possible choice for backsolving. If you decide to backsolve, don’t simply go on automatic pilot and choose (C). Scope out the answers, and see if one stands out as a much easier choice for backsolving calculations: if there is such answer choice available, chances are very good that the question-writer placed it for just that purpose.

Summary

If you have any questions about what I have said here, or if you would like to add anything, please use our comments section below.

Practice problem explanations

Q1. We’ll use backsolving. Start with choice (C). If x = 4, then

4^3 + 5*4 = 64 + 20 = 84

That’s just larger than 80, so this may well be the answer. We have to verify that x = 3 is below 80:

3^3 + 5*3 = 27 + 15 = 42

That’s well below 80, so x = 4 is the lowest integer for which the expression is greater than 80.

Answer = (C)

Q2. First of all, 1\% of \${200,000} is \${2000}, and six times this means 6\% is \${12,000}. That’s the easy part of the problem. Now we know 14.5\% of revenue is \${12,000}.

As we discussed in this post, starting with (C) in this problem would not be fun. Instead, we’ll backsolving starting with the round number, choice (D). Suppose revenue = \${80,000}.

(a) 1\% of \${80,000} = \${800}

(b) 10\% of \${80,000} = \${8,000}

(c) Multiply (a) by 4: 4\% of \${80,000} = \${3,200}

(d) Divide (a) by half: 0.5\% of \${80,000} = \${400}

(e) add (b) & (c) & (d): 14.5\% of \${80,000} = \${11,600}

That’s a bit shy of the required \${12,000}, so revenue must be larger than \${80,000}. That leads up immediately to the last choice.

Answer = (E)

Q3. We’ll use backsolving. Start with choice (C). If price = 48, then

department pays \${4} less than half = \${24} - \${4} = \${20}

HR pays \${1} more than a third = \${16} + \${1} = \${17}

Together, they pay \${37}, leaving Harold to pay the remaining \${11}. Harold pays a bit too much, so the price must be a bit less. We strongly suspect that (B) will work, but we have to verify that assumption.

Try (B). If price = \${42}, then

department pays \${4} less than half = \${21} - \${4} = \${17}

HR pays \${1} more than a third = \${14} + \${1} = \${15}

Together, they pay \${32}, leaving Harold to pay the remaining \${10}. This works.

Answer = (B)

Q4. As we discussed in this post, starting with (C) in this problem would not be fun. We’ll backsolving starting with a round number. The answers give us two round numbers, choice (B) and choice (E). Let’s think strategically about this. If we try (E) and it works, then we have the answer, but if it doesn’t work, we would know the amount would have to be less, but we can already see that. Backsolving with (E) does not necessarily give us a lot of information.

Instead, backsolving with (B). Let’s say Jackson puts \${120,000} in P and \${180,000} in Q.

In P, Jackson earns 12\% of \${120,000}

10\% of \${120,000} = \${12,000}

1\% of \${120,000} = \${1,200}

2\% of \${120,000} = \${2,400}

12\% of \${120,000} = \${14,400}

In Q, Jackson earns 25\% of $180,000}

50\% of \${180,000} = \${90,000}

half of that: 25\% of \${180,000} = \${45,000}

Total \space interest \space earned = \${14,400} + \${45,000} = \${59,400}

Not quite enough interest. To earn that extra \${600} of interest that would bring the total interest up to \${60,000}, Jackson would have to have taken money out of P, which earns less interest, and have put it in Q, which earns more interest. That means, the amount in Account P must be less than \${120,000}. That leaves only one answer.

Answer = (A)

Q5.

We start with 200 ml of solution X. Because solution X is 10\% alcohol by volume, then we must have 200 * .1 = 20 ml of alcohol. Likewise, we must have 200 - 20 = 180 ml of water.

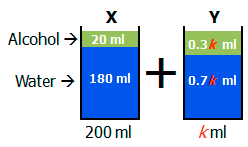
We then add an unknown amount of solution Y to this. Let's call the unknown amount 'k'. Because solution Y is 30\% alcohol by volume, the amount of alcohol must be 0.3k \space ml. Also, the amount of water must be 0.7k \space ml.

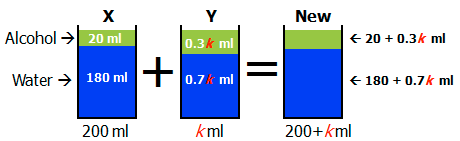
Combining solution X with solution Y yields a new solution that is 25\% alcohol by volume. The total volume of this new solution must equal the sum of its parts: 200 ml + k \space ml. Similarly, the volume of alcohol must equal the sum of its parts: 20 ml + 0.3k \space ml. Likewise, the volume of water must equal the sum of its parts: 180 ml + 0.7k \space ml.

Now, let's set up a ratio that demonstrates the new solution is 25\% (or \dfrac{1}{4}) alcohol by volume:

\dfrac{1}{4}=\dfrac{20+0.3\red{k}}{200+\red{k}}

From here, we can cross-multiply and solve for k:

1(200+\red{k})=4(20+0.3\red k)

200+\red k = 80+1.2 \red k

120=0.2 \red k

600=\red k

Answer = (E)