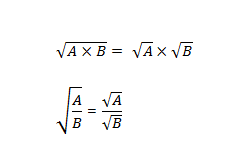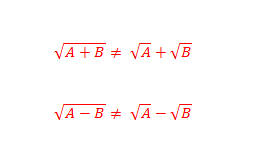Simplifying Radical Expressions

Practice Questions

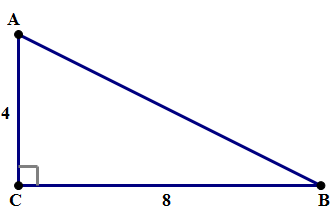
Q1. Find the length of AB

A. 4\sqrt{3}

B. 4\sqrt{5}

C. 8\sqrt{2}

D. 8\sqrt{3}

E. 12

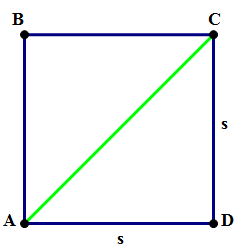
Q2. Find the length of AB

A. 4\sqrt{2}

B. 4\sqrt{3}

C. 8\sqrt{6}

D. 8\sqrt{3}

E. 8\sqrt{6}

The geometry of those questions is not too difficult, but the trick is how to handle those radicals. If that befuddles you, this is just the post for you.

Distributing radicals

First of all, we need to review some rules for square-roots. We can distribute a square-root over multiplication or division. We cannot distribute a square-root over addition or subtraction. Another way to say that: we can separate a square-root by multiplication or division, but not by addition or subtraction.

Beware of those two on the right: they are very tempting mistakes, and QUANT questions will be designed specifically to elicit that mistake.

Simplifying radicals

Suppose we want to simplify \sqrt{72}, which means writing it as a product of some positive integer and some much smaller root. In order to do this, we are going to use the first property given in the previous section: we can separate the square-root by multiplication. The trick is: for 72, find any factor which is a perfect square. For example, 72 = 9*8, and 9 is a perfect square. Therefore

\sqrt{72} = \sqrt{9 \times 8} = \sqrt{9} \times \sqrt{8} = 3\sqrt{8}

We have simplified, but not all the way, because 8 still has another factor, 4, which is a perfect square. To continue:

\sqrt{72} = 3\sqrt{8} = 3\sqrt{4 \times 2} = 3\sqrt{4} \times \sqrt{2} = 3 \times 2 \times \sqrt{2} = 6\sqrt{2}

That last expression is fully simplified, because the number under the radical, 2, has no factor greater than 1 that is a perfect square. (You always are guaranteed the radical is as simple as it’s going to get if the number under the radical is prime.) That simplification took a relatively large number of steps. We would have been more efficient if we had noticed at the outset: 72 = 36*2. Then:

\sqrt{72} = \sqrt{36 \times 2} = \sqrt{36} \times \sqrt{2} = 6\sqrt{2}

It saves you a bit of time if you happen to factor out the largest possible perfect-square factor right at the beginning, but as this process shows, that’s not strictly necessary for arriving at the correct simplification.

Having seen this, you may want to give the practice problems another go before looking at the explanations below.

Practice problems solutions

Q1. First of all, we use that most amazing theorem, the Pythagorean Theorem.

(AB)^2 = (AC)^2 + (BC)^2

(AB)^2 = (4)^2 + (8)^2 = 16 + 64 = 80

That’s the easy part. Now, we have to take a square-root of 80. Notice that 80 = 16*5 (16 is the largest perfect-square factor of 80).

AB = \sqrt{80} = \sqrt{16 \times 5} = \sqrt{16} \times \sqrt{5} = 4\sqrt{5}

Answer = B

Q2. There are a few dozen ways to approach this. Consider the square:

We know that s^2 = 48. Let’s not simplify that, but just leave that as is. You see, we are going to use the Pythagorean Theorem again, in the right triangle ACD, so even if we found out the square-root of s, we would have to turn around and square it again anyway.

(AC)^2 = (AD)^2 + (CD)^2

(AC)^2 = s^2 + s^2

(AC)^2 = 48 + 48

(AC)^2 = 96

AC = \sqrt{96}

Again, the meat of the problem involves simplifying this radical. Notice that 96 = 16*6.

AC = \sqrt{96} = \sqrt{16} \times \sqrt{6} = 4\sqrt{6}

Answer = C