Geometry Diagram Assumptions

What can you assume on GRE geometry diagrams, and what can’t you assume? First, here are a couple of practice questions.

Q1.

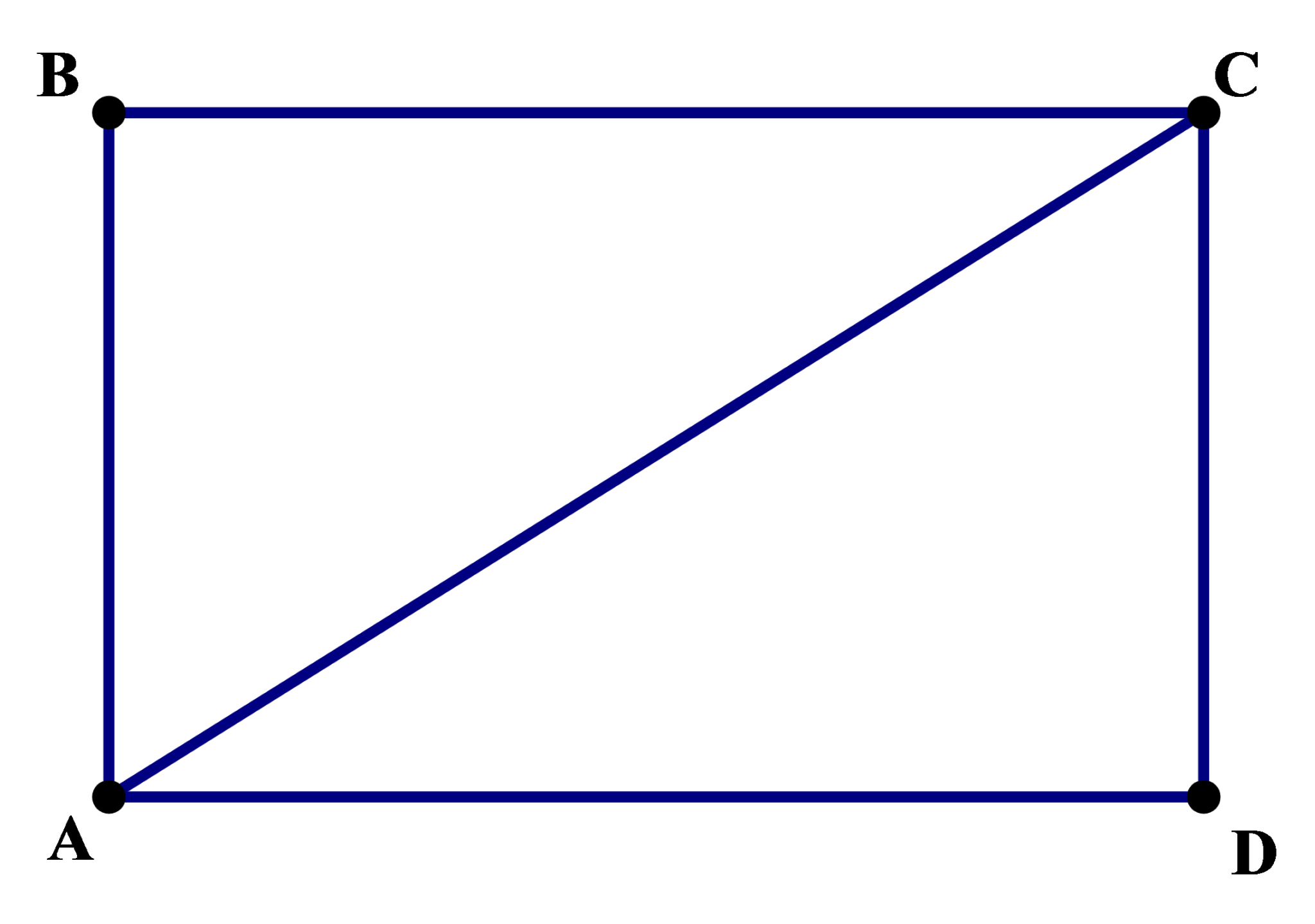
Quadrilateral ABCD is a rectangle.

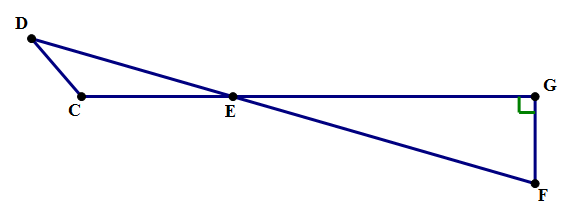
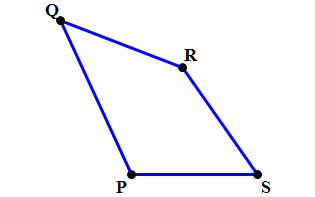
Q2.

What you can’t assume on GRE geometry problems

The biggie is: no diagram is drawn to scale. That means — if nothing is specified about the lengths, then any lengths may be the longest or shortest lengths of the diagram. It also means that any angle that is not marked could be acute, right, or obtuse. For example, if this diagram appears without further comment —

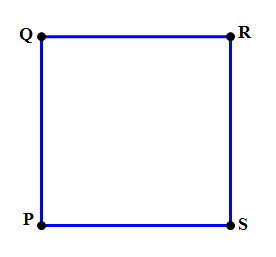
.. then it is cruelly and deceitfully trying to tempt you into believing that it is really a square. If this were a square, then you would know a whole boatload of things (four congruent sides, four right angles, congruent & perpendicular diagonals, etc.) The great unwashed masses taking the GRE will fall into this erroneous assumption, and all its implications, like lemmings running to the sea. In fact, because the diagram specifies no lengths or angles, it could be any one of the following:

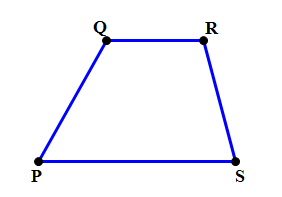
You always have to have your visual imagination warmed up for possible alternatives, with different lengths and different angles. Any angle could be the largest or smallest angle. Any side could be the largest or smallest side. The shape could look not even vaguely like the explicit diagram that appears. That’s all fair game in the GRE’s blanket statement: “no diagram drawn to scale.”

If angles appear to be right angles, you can’t assume they are right angles unless the test says so, or unless a little “perpendicular square” appears in the diagram. For example, in #1 above, the text specifies that the figure is a rectangle, so this means you can assume it has all the properties of rectangles (four right angles, congruent opposite sides, etc.) In #2, \angle{EGF} is marked with the little perpendicular square, so we are guaranteed that \angle{EGF} = {90}\degree. If nothing is marked or specified, you are falling into a trap to assume that an angle that looks right in the diagram truly is right.

If lengths appear equal, they may not be. If JK appears longer than WX, then the relationship may be that way, or they may be equal, or it may be that WX is in fact longer that JK. If lines appear parallel or perpendicular, you cannot assume either if it’s not specified. You should always be suspicious about a GRE geometry diagram, and the less that is specified in words, the more suspicious you should be.

What you can assume on GRE geometry problems

The most fundamental thing you can assume about any geometric diagram: any line or line segment that looks straight, is straight. For example, in problem #2 above, we are absolutely guaranteed that D-E-F are collinear and that C-E-G are collinear — that those two are straight lines with no “hidden bend” at point \space E. If it looks straight, it is straight.

BTW, don’t confuse “straight” (meaning, “lying in a line, collinear”) with “horizontal.” Many people say “straight” when they mean “horizontal”, and this is a 100\% wrong mistake that leads to a great deal of confusion. For example, you must assume a line on the GRE is “straight”, but you absolutely cannot assume it is “horizontal” if that is not stated.

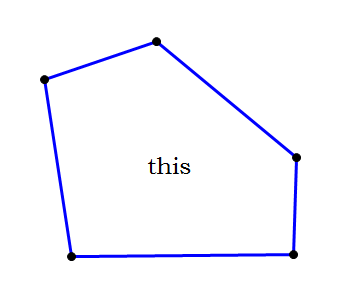
If you are told a shape in a GRE diagram is a polygon in general or a particular kind of polygon (triangle, rectangle, etc.), then you can assume

(a) it is a closed shape:

(b) that the sides don’t “cross” each other and that the figure is “convex” (all vertices pointing outward), not “concave” (some vertices pointing inward).

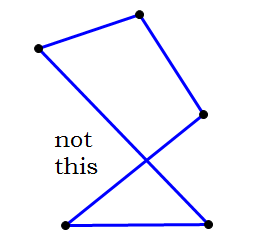
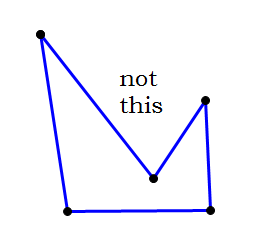
Finally, it’s important to know the theorems and the defined properties of shapes. For example, if you are told that two angles in a triangle are equal, then by that extraordinary theorem, the Isosceles Triangle theorem, you also know the two opposite sides are congruent. If you are told that a figure is, say, a rhombus, then you automatically know it has all the defined properties of a rhombus (four congruent sides, congruent opposite angles, perpendicular diagonals). Technically, if you know something as the result of a definition or a theorem, then you are deducing it, not assuming it, but this is still in the broad categories of things you need to know about your diagram that were not explicitly stated.

Summary

Be very clear on what you can assume and what you can’t assume — I would guess that over 80\% of all the mistakes that folks make on GRE Geometry problems involving diagrams result from improper assumptions. It may pay to go back to the practice questions above and re-evaluate them in terms of what you have learned here. Here’s a further practice question:

Practice question explanations

1) In this question, we are guaranteed that it’s a rectangle, which substantially reduces the range of possible shapes. Notice, though, we know absolutely nothing about the relative lengths of the two sides — either one could be much larger than the other. It’s good to visualize two versions, one with each of the sides exaggeratedly longer than the other:

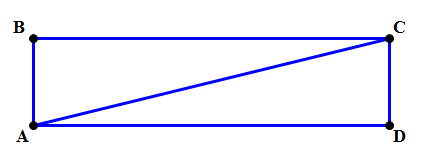
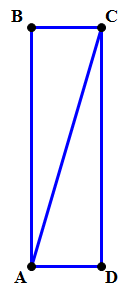
In the version on the left (AD \gt AB), it’s clear that \dfrac{AC}{AB} is much much bigger than 1, may be equal to 5 or 6, while \dfrac{AB}{AD} is small, only say about \dfrac{1}{5}. In that version, column A definitely would be bigger.

Meanwhile, in the version on the right (AB \gt AD), now \dfrac{AC}{AB} is still larger than 1, but here just larger than 1 — maybe \dfrac{6}{5} or \dfrac{7}{6}, much less than 2 — and now \dfrac{AB}{AD} is very large, maybe 4 or 5. In this version, column B would be bigger.

Because the diagram can be changed to make either column bigger, we cannot draw any conclusions.

Answer = D

Answer = C