Isosceles Triangles

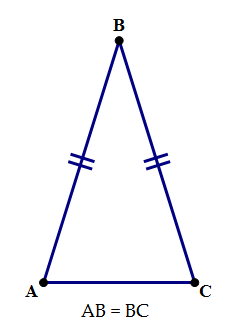
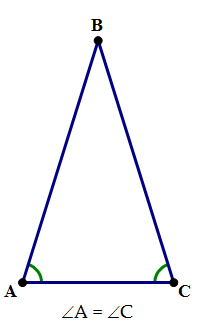
The quantitative section asks, among other things, about geometry. One of the QUANT’s favorite figures is the isosceles triangle. An isosceles triangle is one that has two congruent sides. Knowing simply that about a triangle has profound implications for answer QUANT Problem Solving & Data Sufficiency questions.

Euclid’s Remarkable Theorem

Euclid first proved this theorem over 2200 years ago. The theorem says:

If the two sides are equal, then the opposite angles are equal

and

if the two angles are equal, then the opposite sides are equal.

It can be used for deductions in both directions (logically, this is called a “biconditional” statement”). Another way to say this: a statement about equal angles is sufficient to conclude equal sides; conversely, a statement about equal sides is sufficient to conclude equal angles. Remember that on QUANT Data Sufficiency!

Isosceles Triangles and the {180}\degree Triangle Theorem

Another favorite QUANT geometry fact is that the sum of all three angles in a triangle − any triangle − is {180}\degree. This is particularly fruitful if combined with the Isosceles Triangle Theorem.

Suppose you are told that Triangle ABC is isosceles, and one of the bottom equal angles (called a “base angle”) is {50}\degree. Then immediately you know that the measure of the other base angle is also {50}\degree, and that means the top angle (the “vertex angle”) must be {80}\degree. Knowing the measure of one base angle is sufficient to find the measures of all three angles of an isosceles triangle.

Suppose you are told that Triangle ABC is isosceles, and the vertex angle is {50}\degree. Well, you don’t know the measures of the base angle, but you know they’re equal. Let x be the degrees of the base angle; then x + x + {50}\degree = {180}\degree right 2x = {130}\degree right x = {65}\degree. So, each base angle is {65}\degree. Knowing the measure of the vertex angle is sufficient to find the measures of all three angles of an isosceles triangle.

BUT, if you are told that Triangle ABC is isosceles, and one of angles is {50}\degree, but you don’t know whether that {50}\degree is a base angle or a vertex angle, then you cannot conclude anything about the other angles in the isosceles triangle without more information. That’s a subtle but important distinction to remember on QUANT Data.