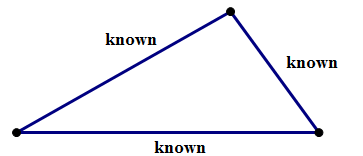
Now, a trip down memory lane. In Geometry, which you probably took early in your high school career, you may remember the four congruence rules. These are rules that absolutely guarantee that two triangles are congruent: if two triangles share this particular combination of traits, there is not any possibility that they could differ in the least. These four congruence rules are known by convenient three letter abbreviations. (Does this ring a bell now?)
I. SSS = Side-Side-Side = if you know the lengths of all three sides of a triangle, that uniquely determines all three angle as well as the shape & size of the triangle. Only one triangle can have those three sides.

II. SAS = Side-Angle-Side (i.e. two sides and the angle between them). Here, you know two of the three sides, and the angle you know is the angle between the two sides. This combination of information is enough to determine unambiguously everything else about the triangle: the other side, the other two angles, the size and the shape. Only one triangle can have this particular combination.
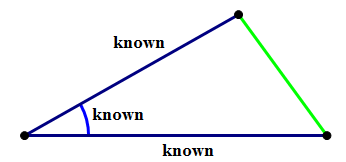
III. ASA = Angle-Side-Angle (i.e. two angles and the side between them). Here, you know two of the three angles, and the side length you know is the one connecting those two vertices. This combination of information is enough to determine unambiguously everything else about the triangle: the other angle, the other two sides, the size and the shape. Only one triangle can have this particular combination.
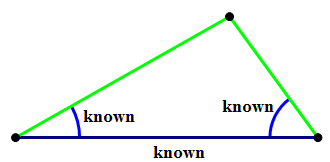
IV. AAS (a.k.a. SAA) = Angle-Angle-Side (i.e. two angles and the side not between them). Here, you know two of the three angles, and the side length you know is one of the two sides not connecting those two vertices. This combination of information is enough to determine unambiguously everything else about the triangle: the other angle, the other two sides, the size and the shape. Only one triangle can have this particular combination.
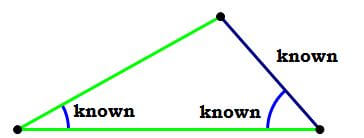
If you have a combination of information that fits into any of those four categories, then that combination uniquely determines the shape and size of the triangle. Every facet of a triangle is fully determined by any of these four combinations.
It’s worth taking a moment just to be clear about the similar sounding combinations of letters, the ones that could be confused with congruence rules, but which actually don’t work.
One is AAA (angle-angle-angle). As it turns out, this is enough to guarantee the shape of the triangle, but because no side is specified, we could scale that shape to any size.
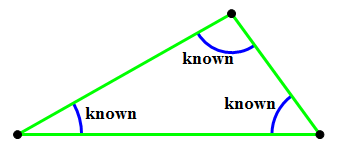
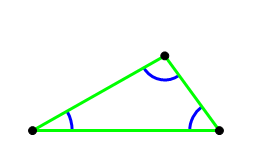
The other involves two sides, and the angle not between those two sides. (I have confidence in your ability to create a three-letter mnemonic to remind yourself that this doesn’t work!) Why this doesn’t work is a tricky issue. The diagram below may illuminate why angle-side-side doesn’t work as a congruence rule, because two different shape triangles can share this particular combination of information.
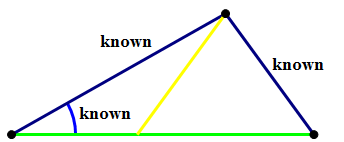
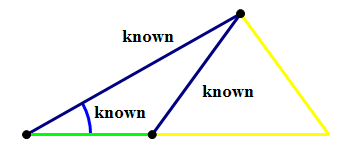
Even if you don’t understand that diagram, it’s enough to know that this combination doesn’t work — it doesn’t guarantee congruence.
OK, great, those are the four congruence rules, but what would they have to do with DS questions on the QUANT? Well, for a start, here’s a PS problem that would never appear on the QUANT.
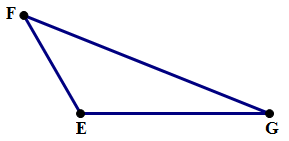
Q1. In the triangle above,
I won’t even bother listing answer choices. The point is: with QUANT math, you simply cannot do this problem. It requires trigonometry to solve, and that’s well beyond what you need to know for the QUANT. That question is
Now, consider this unlikely but hypothetical question, suspiciously similar to #1.

Q2. In the triangle above,
Statement #1:
Statement #2:
Curiously, even though we can’t solve anything, we can still answer the question. The prompt gives us two sides of the triangle.
Statement #1 gives us the third side: that would result in SSS, which uniquely determines a triangle.
Now, forget statement #1. Statement #2 gives us the angle between the two sides given in the prompt, so we now have SAS, which also uniquely determines a triangle.
Both statements are sufficient, so Answer = D. Even though every single relevant calculation was absolutely beyond what we could do with QUANT math, we could still answer the DS question. That’s very important!
Even though a DS question just like this would be “fair game” for GMAC to use, it’s unlikely they would actually give a question like this. Even though you don’t need to solve for numerical answers to figure out a DS question, they almost invariably give questions which could be solved numerically using just QUANT math techniques, so this question is out. Nevertheless, this demonstrates a hugely important strategy point: the congruence rules could provide a ridiculously efficient geometry shortcut on the DS.
Typically, triangle questions of this genre would involve triangles you solve, for example, the special right triangles. Suppose, say, the DS question give you enough information to determine that it’s a 30-60-90 triangle, but either you forget the details of that pattern, or you simply don’t want to go through those calculations if you don’t need to do them. The congruence rules can be an express lane to answering the DS question, a lane that avoids doing any unnecessary calculations — which, of course, should always be your strategy on QUANT Data Sufficiency. If, at any step, the information given matches on of the four congruence rules, then everything about the triangle is thereby determined — in other words, you automatically have sufficiency.
By the way, for the geometrically inquisitive who do want to know the value of
Of course, I give that purely for the entertainment of folks who remember their trigonometry.
Q3. If
(1)
(2)
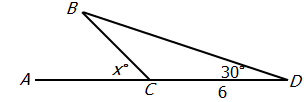
A. Statement 1 ALONE is sufficient to answer the question, but statement 2 alone is NOT sufficient.
B. Statement 2 ALONE is sufficient to answer the question, but statement 1 alone is NOT sufficient.
C. BOTH statements 1 and 2 TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient.
D. Each statement ALONE is sufficient to answer the question.
E. Statement 1 and 2 TOGETHER are NOT sufficient to answer the question.
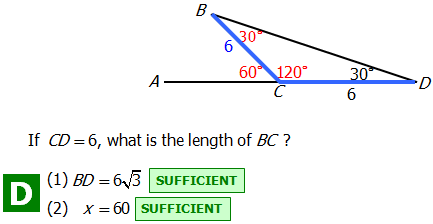
Answer = D
FAQ: Why is statement #1 sufficient?
A: For QUANT data sufficiency questions, we don't actually need to know HOW to calculate the answer. We just need to know that someone could calculate the answer based on the information provided.
In fact, the QUANT will sometimes present you with calculations that you may or may not be able to solve with the expected QUANT level knowledge (trigonometry is above this level), but you should know whether it's possible at all.
From statement #1, we know the length of two sides, and the size of the angel between them. Based on triangle congruence rules, there is only one possible triangle that has these characteristics. So using trigonometry, someone could determine the length of BC.
Don't worry about calculating the specific value. BUT if you love math as much as we do and are interested in understanding the principles behind it, here's a good website to check out.
FAQ: I know we don't have to, but how would we find the length of
A: As mentioned in the prior FAQ, we don't need to know this -- but it's great that you want to learn, and we're happy to provide you with an explanation! Here's a step-by-step explanation.
1. If we draw a line from
2. Using the properties of
3. ED then becomes
4. Therefore,