Adding and Subtracting Powers

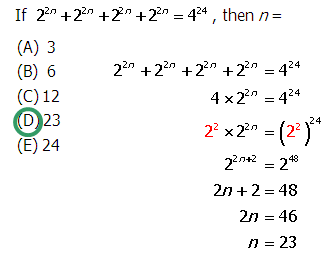
First, consider this practice problem:

Q1. 7^6 + 7^8 =

A. 7^{14}

B. 7^{16}

C. 7^{48}

D. 14^{14}

E. 50*7^{6}

Q2. If 22n + 22n + 22n + 22n = 424, then n =

A. 3

B. 6

C. 12

D. 23

E. 24

Operations with powers

There are legitimate laws of exponents for multiplying and dividing powers. For example:

\bold{\bigg(a^m\bigg) \times \bigg(a^n\bigg) = a^{m+n}} \to \bigg(7^8\bigg) \times \bigg(7^6\bigg) = 7^{8+6} = 7^{14}

\bold{\dfrac{a^m}{a^n} = a^{m-n}} \to \dfrac{7^8}{7^6} = 7^{8-6} = 7^2 = 49

Multiplying powers means add the exponents and dividing powers means subtract the exponents. For more on this, see this Web Page — Exponent Properties.

Alas! There is no law of exponents for adding and subtracting powers. In other words, (a to the n) plus or minus (a to the m) is not going to equal a-to-the-power-of-anything-in-particular. There is no convenient way to combine a sum or difference of powers into a single power expression.

Distributing and factoring out

\bold{\LARGE{a} \times (\LARGE{b} + \LARGE{c}) = \LARGE{a} \times \LARGE{b} + \LARGE{a} \times \LARGE{c}}

That is a rather remarkable and often underestimated equation. First of all, it is a statement of the Distributive Law: if we start on the left and go to the right, we are distributing “a.” The reverse process is called factoring out: if we start on the right side, and go to the left, we are factoring “a” out. Multiplication distributes over addition and subtraction: we could replace both plus signs with minus signs in that equation and it would still be true.

Written in simple variable form, it probably doesn’t look all that earth-shattering, but the implications of that equation are so widespread as to boggle the mind. Addition and subtraction of variables, addition and subtraction of fractions, and all techniques for factoring quadratics are ultimately dependent on this profound fundamental law.

Before discussing the implications for addition and subtraction of powers, I will just make one more point. In this above equation, “a” can be any common factor of the two terms on the right, but in some sense, we “maximize” the effect of factoring out when the factor we factor out is the Greatest Common Factor (the GCF). See this link for a review of how GCF works with numbers.

Factoring out to add & subtract powers

Suppose we want to simplify

2^{17} - 2^{13} = ?

Well, since both terms are powers of two, they share several common factors (2^1, 2^2, 2^3, etc.). The GCF of both of these terms is 2^{13} itself. We can express each term as the product of the GCF and something else.

2^{17} = (2^4)*(2^{13})

2^{13} = (1)*(2^{13})

Now, we can write the difference of powers as

2^{17} - 2^{13} = (2^4)*(2^{13}) - (1)*(2^{13}) = ?

I realize that, at the moment, it may not be completely obvious that this will ultimately be a step in the direction of simplification — it looks like we made everything gratuitously more complex in the second step! Trust that things will simplify soon! Here’s the Distributive Law equation again, now with subtraction and with left & right switched from above.

\bold{\LARGE{a} \times \LARGE{b} - \LARGE{a} \times \LARGE{c} = \LARGE{a} \times (\LARGE{b} - \LARGE{c})}

Notice that the second step of the power subtraction equation matches perfectly the pattern on the left of this statement of the Distributive Law: a = 2^{13}, b = 2^4 and c = 1. Following this pattern, we see this turns into:

2^{17} - 2^{13} = (2^4)*(2^{13}) - (1)*(2^{13}) = (2^{13})*[(2^4) - 1]

Now, it’s germane to point out: we should be able to simplify 2^4.

2^1 = 1

2^2 = 4

2^3 = 8

2^4 = 16

That, in turn, allows us to simplify the piece in the brackets in the last expression:

2^{17} - 2^{13}

= (2^4)*(2^{13}) - (1)*(2^{13})

= (2^{13})*[(2^4) - 1]

= (2^{13})*[16 - 1] = (2^{13})*(15)

Voila! That final expression, fifteen times two to the thirteen, is the simplification of the difference of two powers.

This process would be particularly important if, for example, you were asked to simplify something like:

\dfrac{2^{17} - 2^{13}}{20}

We can’t cancel from either term in the numerator as long as we have addition or subtraction in the numerator, but once we simplify the numerator so that it’s all multiplication, we can cancel. You should verify for yourself that:

\dfrac{2^{17} - 2^{13}}{20} = \dfrac{2^{13}*(2^4 - 1)}{4*5} = \dfrac{\cancel{2^2}*2^{11}*(2^4 - 1)}{\cancel{2^2}*5} = \dfrac{2^{11}*15}{5} = \dfrac{15}{5}*2^{11} = (3)*(2^{11})

A remarkable simplification!

Practice question solution

Q1. The GCF of 7^6 and 7^8 is 7^6.

7^6 = (1)*(7^6)

7^8 = (7^2)*(7^6)

Therefore

7^6 + 7^8 = (1)*(7^6) + (7^2)*(7^6) = (1 + 7^2)*(7^6) = (1 + 49)*(7^6) = (50)*(7^6)

Answer = E

Q2.

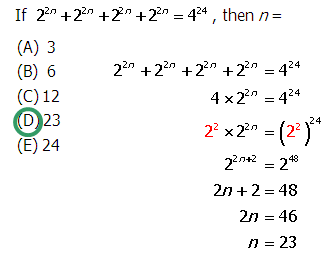
Answer = D