Exponent Properties

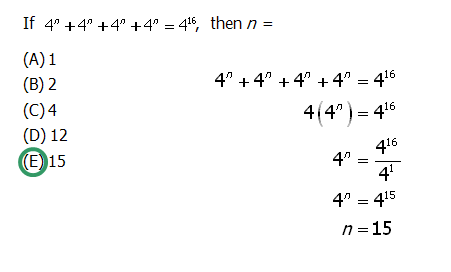
Because of their clarity and concision, the laws of exponents lend themselves well to GMAT math, especially to the Data Sufficiency format. If math isn't your thing, then perhaps the last time you gave any thought to exponents was back in Algebra Two, and perhaps exponents weren't your favorites there either. Take heart! In this post, I will explain the properties you need to know to be successful on the GMAT Quantitative section.

Exponent Properties

Fundamentally, an exponent is how many times you multiply a number, that is, how many factors of a number you have. This is the fundamental definition. The expression 5^4 means: multiply four 5's together. The expression 2^3 means: multiply three 2's together, which gives an answer of 8, so 2^3 = 8. Technically, 2 is the "base", 3 is the "exponent", and 8 is the "power." The action of raising something to an exponent is called "exponentiation."

Distribution

Just as multiplication distributes over addition & subtraction

\LARGE{a \times (b + c) = a \times b + a \times c}

so exponentiation distributes over multiplication and division.

\LARGE{(x \times y)^r = (x^r) \times (y^r)}

Why is that? Well, consider (x \times y)^3. This means the thing in parentheses multiplied by itself three times: (x \times y)^3 = (x \times y) \times (x \times y) \times (x \times y). Well, when we have a bunch of factors, we can rearrange them in any order, because order doesn't matter in multiplication. So, I could rearrange them as follows:

(x \times y)^3=

(x \times y) \times (x \times y) \times (x \times y)=

x \times x \times x \times y \times y \times y=

(x \times x \times x) \times (y \times y \times y)=

\Big(x^3\Big) \times \Big(y^3\Big)

All the laws of exponents make sense if you just go back to the fundamental definition.

In this context, I will say: beware of one of the most tempting mistakes in all of mathematics. Exponentiation does NOT distribute over addition.

\LARGE{(a + b)^n} \not= \LARGE{(a^n) + (b^n)}

Beware. Even when you know this is wrong, even when you make an effort to remember that it's wrong, the inherent pattern-matching machinery of your brain will automatically pull your mind back in the direction of making this mistake. You must be vigilant to avoid this mistake.

Multiplying Powers

What happens when you multiply two unequal powers of the same base?

\LARGE{(x^r) \times (x^s) = ?}

Well, let's think about a concrete example. Suppose we are multiplying (x^5)*(x^3). Well, by the fundamental definition, x^5 = x*x*x*x*x, and x^3 = x*x*x, so

(x^5)*(x^3) = (x*x*x*x*x)*(x*x*x) = x*x*x*x*x*x*x*x = x^8

If we start with five factors of x, and "stir in" three more factors of x, we wind up with a total of eight factors. All we have to do is add the exponents. We can simply generalize this pattern:

\LARGE{(x^r) \times (x^s) = (x^{r+s})}

Don't just memorize this: make sure you understand the logic that leads to it. Remembering with the logic is 100x more effective than blind memorization!

Dividing Powers

What happens when you divide two unequal powers of the same base?

\LARGE{\dfrac{x^r}{x^s} = ?}

As with last time, a concrete example will illuminate the question. Suppose we divide \dfrac{\bigg(x^7\bigg)}{\bigg(x^3\bigg)}. By the fundamental definition, x^7 = x*x*x*x*x*x*x and x^3 = x*x*x, so

\dfrac{x^7}{x^3} = \dfrac{x*x*x*x*x*x*x}{x*x*x} = \dfrac{x*x*x*x*\cancel{x*x*x}}{\cancel{x*x*x}} = x*x*x*x = x^4

If we start out with seven factors, and then cancel away three of them, we are left with four. We just subtract the exponents. We can also generalize this pattern:

\LARGE{\dfrac{x^r}{x^s} = x^{r-s}}

Once again: understand the logic, because remember through understanding is considerably more powerful than blind memorization.

Once again: understand the logic, because remember through understanding is considerably more powerful than blind memorization.

An Exponent of Zero

Mathematicians love to extend patterns. One example of this is the zero exponent. If we just see x^0, we may wonder: how on earth are we going to understand what this could mean? We are clearly outside of the realm where the fundamental definition helps us.

One clever trick we can us is to employ the pattern found in division of powers. Suppose we have \dfrac{(x^4)}{(x^4)} — then, the "subtraction of exponents" would imply:

\dfrac{(x^4)}{(x^4)} = x^{4-4} = x^0

but just fundamental logic would tell us that anything over itself equals one. Therefore, this expression \dfrac{(x^4)}{(x^4)} must have a value of 1. That, in turn, tells us the value of x^0. x^0 =1.

Negative Exponents

Here, we will extend the patterns even further. Consider this chart, for a base of 2:

Each time we move one cell to the right, the power gets multiplied by 2, and each time we move one cell to the left, the power gets divided by 2. That's a very easy pattern to extend to the left:

All we have done was to extend the pattern "move one cell to the left, and the power gets divided by 2." The result, we see, is that negative powers are reciprocals of their corresponding positive powers. This is consistent with the Division of Powers rule: if dividing means subtract the exponents, then an exponent of -3 means we are dividing by three factors of the number. Therefore, the general rule is:

\LARGE{x^{\space{-r}} = \dfrac{1}{x^r}}

Summary

I can't urge enough: the key to remembering these rules is understanding the logic of the arguments behind them. If you understand these rules, you will understand whatever the GMAT throws at you concerning exponents.

Practice Questions

Q1. If \dfrac{8^5 \times 4^6}{16^n}=32^{1-n} then n =

A. -22

B. -11

C. 5

D. 11

E. 22

Explanation:

To solve this problem, it is very helpful to express all of the quantities in terms of the same base. Once we do that, we can make use of the various Laws of Exponents to simplify the quantities further.

First, we'll express all of the quantities in terms of the same base of 2:

\dfrac{8^5 * 4^6}{16^n} = 32^{(1 - n)}

\dfrac{{(2^{3})}^5 * {(2^{2})}^6}{(2^4)^n} = (2^5)^{(1 - n)}

We can now simplify all the powers that are being raised to a power via this Law of Exponents:

\LARGE{\bold{(x^a)^b = x^{ab}}}

\dfrac{2^{(3*5)} * 2^{(2*6)}}{2^{(4*n)}} = 2^{(5*(1-n))}

\dfrac{2^{15}*2^{12}}{2^{4n}} = 2^{(5-5n)}

Next, we can simplify the numerator via this Law of Exponents:

\LARGE{\bold{(x^a) * (x^b) = x^{(a + b)}}}

\dfrac{2^{(15 + 12)}}{2^{4n}} = 2^{(5 - 5n)}

\dfrac{2^{27}}{2^{4n}} = 2^{(5 - 5n)}

We can then simplify the entire fraction via this Law of Exponents:

\LARGE{\bold{\dfrac{x^a}{x^b} = x^{(a-b)}}}

2^{(27-4n)} = 2^{(5-5n)}

Lastly, we'll use the following rule to solve for n:

"If two powers with the same base are equal, then the exponents must be equal. That is, if b^x = b^y, then x = y, provided that b does not equal 0 or +/-1."

27 - 4n = 5 - 5n

n = 5 - 27

n = \bold{-22}

Answer = A

Q2. If 4^n + 4^n + 4^n + 4^n = 4^16, then n =

A. 1

B. 2

C. 4

D. 12

E. 15

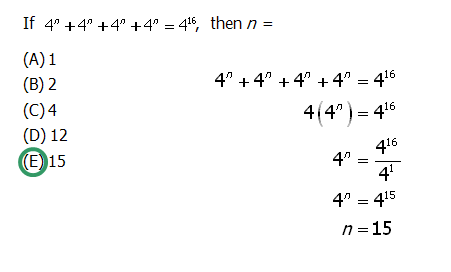
Answer = E

Q3. If x and y are positive odd integers, then which of the following must also be an odd integer?

I. x^{y+1}

II. x(y+1)

III. (y+1)^{x-1} + 1

A. I only

B. II only

C. III only

D. I and III

E. None of the above

Explanation:

Case I: Since x and y are both positive odd integers, x^{(y+1)} becomes (odd)^{(odd + odd)}, which becomes (odd)^{even}. Multiplying any number of odd numbers together always results in an odd number.

This case is acceptable.

Case II: x^{(y + 1)} becomes (odd)^{(odd + odd)}, which becomes (odd)^{(even)}. Any odd number times an even number results in an even number.

This case doesn't work.

Case III: The portion (y + 1)^{(x - 1)} becomes (odd + odd)^{(odd - odd)}, which becomes (even)^{even}. For our whole expression, we are now left with (even)^{even + 1}, which is (even)^{even + odd}.

There are actually two different possibilities that arise from this setup. For most cases, we'll get an odd number in the end. For example:

2^2 + 1= 4 + 1 = 5 (odd)

4^4 + 1 = 256 + 1 = 257 (odd)

etc.

However, zero is also an even number, and anything raised to the power of zero results in 1. Because of this, we can end up with an even number as the result of our expression:

2^0 + 1 = 1 + 1 = 2 (even)

4^0 + 1 = 1 + 1 = 2 (even)

etc.

Since we can end up with both even and odd numbers from this case, this case doesn't work.

Only Case I guarantees an odd integer.

Answer = A