
Often, when we talk about triangles in the context of the QUANT, we focus on right triangles (a relatively elite category) or the special right triangles (viz.
But just as there are many more people who don’t live in the Hamptons than do, just as there are many more former Major League Baseball players who aren’t in the Baseball Hall of Fame then those who are, so there are many more non-right triangles than right triangles. This is a post about them, about the
Well, first of all, the sum of the three angles of any triangle is
That has a scary sounding name, doesn’t it? It sounds really sophisticated. In fact, it’s an idea so simple that a small child could understand the basics. Formally, it says: the sum of any two sides of a triangle must be greater than the third. In picture form:

The Triangle Inequality produces these three inequalities for any triangle. Now, think about why this has to be true. The shortest distance between
Just as a political discussion of “the
The Side Angle Inequalities. First, the technical way to say it: the measures of the three angles of a triangle are unequal in the same order as the lengths of theiropposite sides. That’s difficult to understand. Next, a picture:

Now, the really down-to-earth, straightforward way to say the idea is: the biggest side is always opposite the biggest angle, and the smallest side is always opposite the smallest angle. (In fact, they only reason I mentioned those other complicated ways to say it was to give you the challenge of figuring out why they just say the same thing as the simple bold statement.)
Those two mathematical patterns, the Triangle Inequality and the Side-Angle Inequalities, are true for all triangles — both the elite and not-elite triangles. On QUANT Math, these are two particularly handy facts to have in your back pocket, especially on Data Sufficiency, precisely because they are true for every triangle under the Sun.
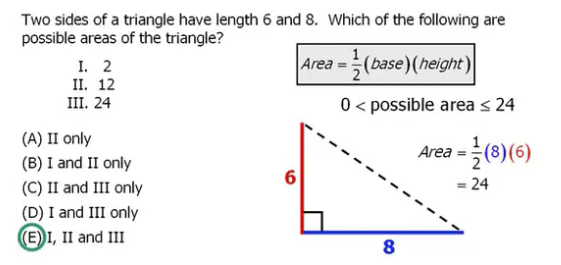
Q1. Two sides of a triangle have length 6 and 8. Which of the following are possible areas of the triangle?
I. 2
II. 12
III. 24
A. I only
B. I and II only
C. II and III only
D. I and III only
E. I, II, and III
This requires a picture explanation. Consider the leg of 6 and the leg of 8 attached at a "hinged" joint at B.

Here, the angle is made very narrow, only 1/100 of a degree. The area of this triangle would be 0.00419 --- you don't need to be able to calculate something like this for the test. The point is -- if the angle were one millionth, or one billionth, the area could be really really small --- greater than zero, but a really tiny decimal. So, clearly, the area can be less than two.
Here, I moved the legs of 6 and 8 apart a little, and produced a triangle with an area of exactly two:

Again, you don't have to know how to build a triangle like this: this is just to show you that it is, indeed possible.
As we increase the angle, we get triangles with more and more area. You do not need to know how to find these areas --- this is just to demonstrate that the area would increase.



Now, there's a geometry theorem that states, when the angle is 90°, the area of the triangle will be a maximum. At that point, the length of 8 will be the base, and the length of 6 will be the height, so the area = 0.5*bh = 24, the maximum possible area.
Thus, the triangle can have all three areas: I, II, and III.
Answer (E).
FAQ: How can the area of the triangle be 2? As per the third side rule, the unknown side must be less than the sum of the other two sides and greater than the difference, so the third side must be 2 < x < 14.
A: For any triangle, if you are given two sides, the third side must be greater than the positive difference of those two sides, but less than the sum of those sides. For this triangle, we are given sides of 6 and 8. We know the third side must be less than 6 + 8 = 14 and greater than 2. Even though our third side must be greater than 2, we can still make the area of the triangle infinitely close to zero, which the second diagram of the explanation demonstrates.
Note: the third side doesn't have to be of integer length. So it could be as small as 2.0000000000001 (or smaller) or as large as 13.9999999999999... (or larger) as long as it's greater than 2 exactly and less than 14 exactly.
When you free yourself of the restriction of integer measures, you can make a triangle with an area of two and still follow the geometric rules. :)
FAQ: If the shortest side of the triangle must be greater than 2, how is it possible to have a height that’s so close to zero?
A: Imagine you have a stretchy string that is placed on top of a line on the ground that measures exactly 8. You pinch the string so that your hand divides the string and on one side is exactly 6 units of length and on the other side is exactly 2 units. It's not a triangle yet, but now pull that stretchy string up an infinitely small amount. You have created a triangle with a base of 8 and a height infinitely close to zero. Note that the height can be much smaller than the shortest side of the triangle! You’ll also notice that the third side is greater than 2—albeit by an infinitely small amount, but greater than 2 nonetheless.
Since we can make an area infinitely close to zero, we know we can make a triangle of any area greater than 0 and less than or equal to the maximum area, which is 6 * 8 / 2 = 24.
If you want to look at real numbers, consider this:
Side 1 = 2.01
Side 2 = 6.00
Side 3 = 8.00
ide 1 and side 2 have a total length of 8.01 (2.01 + 6.00). So the two sides combined are just slightly longer than side 3. If you try to draw a triangle like this, you'll notice that the height has to be very very small because the sides 1 and 2 are only 0.01 longer than side 3. Now imagine a triangle that has sides (2.000001, 6, and 8). The height would be even smaller. Ultimately, you can keep shrinking the 3rd side until the height is almost 0.
FAQ: Why did we choose 8 for the base, and not 6?
A: Which side of the triangle we choose for the base is arbitrary: it doesn’t change the area of the triangle. We could follow the same process with 6 as the base, and we would get the same result for both the minimum and maximum areas of the triangle. For instance, as long as we know that a right triangle would give us the maximum area, we find the same answer: 8 * 6 / 2 and 6 * 8 / 2 are both 24, and that's as big as the triangle can get.
FAQ: Why do we choose a right triangle?
A: Good question! The area of a triangle is maximized when the triangle is a right triangle. If we have an acute or an obtuse triangle, that non-90 degree angle changes the shape of the triangle and we end up losing some height in the process.
Q2. The lengths of the sides of triangle ABC are such that AB = x + 2, BC = x - 3, and AC = y - 1. Which angle in triangle ABC is the largest?
(1) x - y = 1
(2) y = 8
A. Statement 1 ALONE is sufficient to answer the question, but statement 2 alone is NOT sufficient.
B. Statement 2 ALONE is sufficient to answer the question, but statement 1 alone is NOT sufficient.
C. BOTH statements 1 and 2 TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient.
D. Each statement ALONE is sufficient to answer the question.
E. Statement 1 and 2 TOGETHER are NOT sufficient to answer the question.
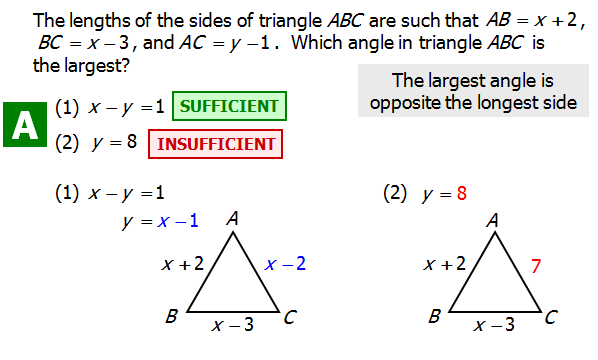
Answer (A).