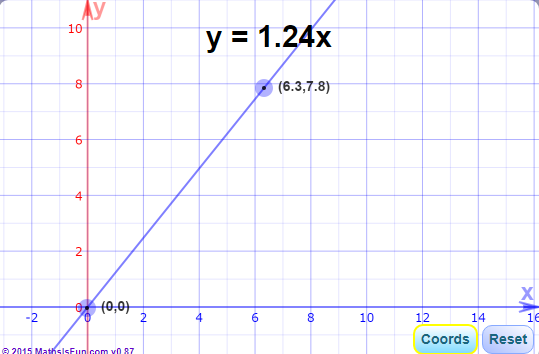
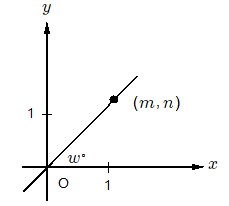Line \bold{\LARGE{y = mx}}
What does it stand for?
y = how far up
x = how far along
m = Slope or Gradient (how steep the line is)
b = the y Intercept (where the line crosses the y axis)
How do you find "m" and "b"?
b is easy: just see where the line crosses the y-axis.
m (the Slope) needs some calculation:
\bold{m = \dfrac{\text{Change in} \space y\text{-axis}}{\text{Change in} \space x\text{-axis}}}
Knowing this we can work out the equation of a straight line:
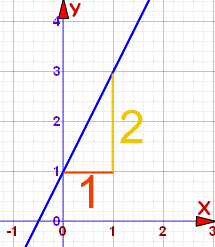
Example 1
m = \dfrac{2}{1} = 2
b = 1 (where the line crosses the y-Axis)
So: y = 2x + 1
Example 2
m = \dfrac{-3}{1} = -3
b = 0
This gives us y = -3x + 0
We do not need the zero!
So: y = -3x
Rise and Run
Sometimes the words "rise" and "run" are used.
\bold{Rise} is how far up
\bold{Run} is how far along
And so the slope "m" is:
\bold{m = \dfrac{rise}{run}}
You might find that easier to remember
Important Fact
if the |slope| (absolute value) of the line is greater than 1, then the angle of the line with x-axis greater than 45\degree
if the angle of the line with x-axis greater than 45\degree, then the |slope| (absolute value) of the line is greater than 1
Practice Question
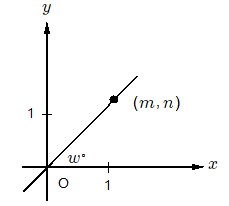w \gt 45| Quantity A | Quantity B |
| m + n | 2m |
A. The quantity in Column A is greater
B. The quantity in Column B is greater
C. The two quantities are equal
D. The relationship cannot be determined from the information given
The equation for a line is:
\bold{y = kx + b}
where m is the slope and b is the y-intercept. Here, we are told that the line passes through the point \space (0,0) and point \space (m,n).
for m and n, we find that: m \gt 1 and n \gt 1, it is obvious that m \not = 0 and n \not = 0
Passing point \space (0,0) means that the y-intercept is 0. So the formula for line k is:
\bold{y = kx}
In order to compare A and B, let's try to subsract A by B:
m + n - 2m = n - m
So the question is to compare m and n.
w \gt 45\degree \to n \gt m, so
Answer is (A)
