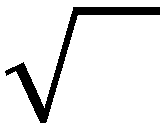
Answer = D
This is a potentially tricky topic. First, consider these practice questions.
Q1. Which value(s) of
I.
II.
III.
(A) I
(B) III
(C) I & II
(D) I & III
(E) I, II, & III
Q2. What is the value of
Statement #1:
Statement #2:
Q3. If Ed's annual salary is
(1) The sum of Rick's annual salary and Jim's annual salary is equal to Ed's annual salary.
(2) The sum of Rick's annual salary and Ed's annual salary is equal to twice Jim's annual salary.
A. Statement 1 ALONE is sufficient to answer the question, but statement 2 alone is NOT sufficient. B. Statement 2 ALONE is sufficient to answer the question, but statement 1 alone is NOT sufficient. C. BOTH statements 1 and 2 TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient. D. Each statement ALONE is sufficient to answer the question. E. Statement 1 and 2 TOGETHER are NOT sufficient to answer the question.A full discussion of these problems will come at the end of this article.
Consider the following, very simple algebra equation
Of course, this equation has two solutions,
Many folks might think this is, in all respects, the same as the solution in the first process — i.e. "taking the square root." We need to draw a subtle distinction here, concerning the nature of this sign:
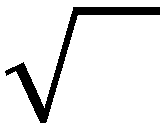
The benighted unfortunately will refer to this as a "square root" sign, but that is a misleading partial name. The name of this simple is the "principal square root" sign, where the word "principal", in the sense of "main" or "primary", here means the positive root only. Accordingly, the output of this sign is always positive.
The number
When a squared algebraic expression appears in a problem, and we ourselves, in the process of problem-solving, find a square root, we need to include all roots, positive and negative (a common mistake is to forget the negative roots). BUT, when the symbol above, the principle square root symbol, is printed on the page as part and parcel of the given problem, this means its output will always be positive.
Thus, the paradoxical juxtaposition
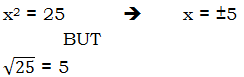
By "equation with a radical", I will be referring to any algebraic equation in which some of the algebra is under a radical sign, a.k.a a principal square root sign. The general strategy for such an equation is
(a) isolate the radical (i.e. get it alone by itself on one side of the equation);
(b) square both sides, thus eliminating the radical; and
(c) solve what remains using algebra (often, this will involve factoring a quadratic.)
All well and good, but there's a catch.
You see, when you square both sides of equation, sometimes that creates solutions that weren't part of the original equation. Consider the hyper-simple equation
We have to square both sides to solve an equation with radicals, but doing so introduces the possibility of an extraneous root. Thus, an essential part of solving any equation with radicals is to check the answers you find, in order to ascertain whether any are extraneous roots. We verify the roots by plugging them into the original equation — if the number does not solve the original equation, as given in the problem, then it is not a bona fide solution.
BTW, just as a general point of strategy, regardless of whether radicals are involved, I recommend checking any algebra values you find by plugging them back into the original equation given in the problem, when possible. It's just a good habit to check your work.
Extraneous roots play a role in both of the sample problems above. Having read this post, you may want to go back and give them another attempt before reading the solutions below. Questions? Let us know in the comment section at the bottom.
Q1. The radical is already isolated, so square both sides.
preliminary solutions:
At this point, an unsuspecting student might be tempted to answer (C), the trap answer. BUT, the problem is: one or both of these answers could be extraneous. We need to check each by plugging back into the original expression.
Check
left side:
right side:
The value
Answer = (B)
Q2. Start with the easier statement, Statement #2.
Statement #2:
Since there are two values of
Statement #1:
The radical is already isolated, so square both sides.
Lo and behold! We have arrived at the same equation we found in Statement #2, with solutions
Test
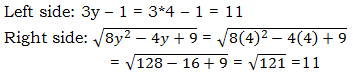
This value checks —
Test
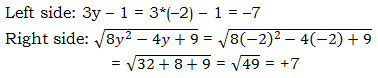
The two sides are not equal, so this does not check! This value,
Thus, the equation given in Statement #1 has only one solution,
Answer = (A)
Q3.
This question is dealing with systems of equations. It wants us to decide if we can determine Rick's salary based on Ed's salary (
It's helpful to start with some variables, so let's make
Let's walk through the statements to see if they are sufficient for determining the value of
1) The sum of Rick's annual salary and Jim's annual salary is equal to Ed's annual salary
We can create an equation from this:
But we've run into a problem. We can't solve for an equation when we have two variables, unless we know more about their values. So this is a dead-end—we can't solve for
Now let's look at 2).
(2) The sum of Rick's annual salary and Ed's annual salary is equal to twice Jim's annual salary.
We can create an equation from this as well:
When we plug in Ed's salary, we get:
Again, we have an equation with two variables, which puts us in another dead end. Therefore, we can't solve for R based on 2) alone.
But what happens if we combine the two statements, and therefore the two equations?
We end up with:
Technically we don't need to do any more work here, because all we need to do is prove that we need both equations to solve for
However, here is how we could show our work to solve for
Multiply the first equation by
Add the two together. The
Thus, we know that Rick's salary is
Answer = (C)