Integer Properties

What are the “properties of integers”?

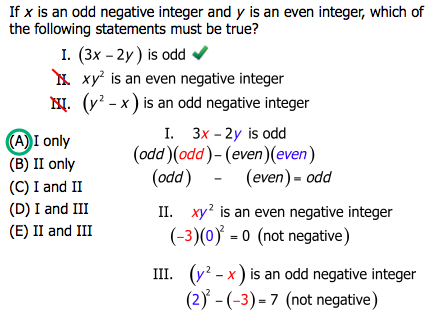
Probably none of these are brand new to you — in fact, you probably learned about all these in grade school. Here’s a list.

a) factors and multiples; GCF and LCM

b) quotient and remainder

c) even & odd

d) prime numbers

e) consecutive numbers and other consecutive sets (odds, evens, multiple of 5, etc.)

f) special properties of 1 (e.g. 1*(any \space number) = that \space number)

g) special properties of 0 (e.g. (any \space number) + 0 = that \space number, (any \space number)*0 = 0)

Again, nothing here is anything that is not covered in grade school, but the trick is: you have to have this all at your fingertips when you take the QUANT. These interrelated concepts lend themselves effortlessly to a myriad of PS & DS questions, and you need to handle them deftly with precision. See this webpage: math factors for tips about factors, multiples, GCF, and LCM. For more tips, see below.

What are integers?

Integers are positive and negative whole numbers. They are the set:

\{... -3, -2, -1, 0, 1, 2, 3, ...\}

They go on forever in the positive and negative direction. They do not include fractions, decimals, and numbers like pi. One way for non-mathy folks to remember the integers: the word “integer” shares a root with the word “integrity” — both come from the Latin word for “whole, wholeness.” If I have integrity, there is a wholeness among my intention, my speech, and my actions; people who lack integrity say one thing and do another.

Big QUANT idea: if the QUANT makes a numerical statement (e.g. x \lt 3), do not assume x is an integer unless that is specified. That’s one of the biggest DS traps, assuming the only possibilities are integers when there are many more possibilities allowed. Here’s a trippy advanced math idea: the infinity of non-integers is infinitely bigger than the infinity of integers. (Read if you are up for an adventure learning about infinity — well beyond what you need to know for the QUANT).

Even and Odd

First of all, here are three addition rules:

1) (even) + (even) = (even)

2) (odd) + (odd) = (even)

3) (even) + (odd) = (odd)

Those also work if the addition sign is changed to a subtraction sign.

Now, three multiplication rules

1) (even)*(even) = (even)

2) (odd)*(odd) = (odd)

3) (even)*(odd) = (even)

(These rules are not the same if the multiplication sign is changed to division!) If you have trouble remembering these six rules, you can always use even = 2 and odd = 3 to remind yourself. (Yes, 1 is also odd, but I recommend not using that as a test number only because it has so many special properties.)

Keep in mind: zero is an even number. Keep in mind, also: negative numbers can be even and odd, just like their positive compatriots. Fractions and non-integers cannot be even or odd: it’s exclusively an integer property.

Prime

Every number has 1 as a factor. Every number has itself as a factor. A number is prime if it has only those two factors, i.e., no factors other than 1 and itself. Only positive integers are said to be prime; we do not apply the distinction “prime” or “not prime” to negative integers, zero, or to non-integers.

Here is a list of the first few primes:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ...

The primes go on forever in an irregular pattern, the nature of which involves the hardest unanswered question in math today, the Riemann Hypothesis — again, well beyond what you need to know for the QUANT. It would be good to memorize that list of the first ten prime numbers: that will help you a lot on the QUANT. Notice that, for a variety of reasons with which we need not concern ourselves here, 1 is not a prime number. Notice, also: 2 is the only even prime number: all other even numbers are divisible by 2. That’s a very handy distinction, especially in QUANT DS: 2 is the only even prime number.

See the factors post for more information about prime numbers.

Know Them Cold

Probably there’s nothing brand new in this post. Probably you have at least a dim memory, if not a perfectly clear understanding, of everything here. Whatever here is rusty, whatever is less than perfectly fluent, you need to practice until you know it cold. The QUANT is relentless in asking about these properties, and if you can nail them every time, you will be well on your way to a stunningly successful QUANT Quantitative section.

A couple of practice questions:

Q1.

If x and y are consecutive odd integers such that x \lt y, what is the value of y + x?

(1) The product of xy is negative.

(2) The sum x + y is the square of an integer.

A. Statement 1 ALONE is sufficient to answer the question, but statement 2 alone is NOT sufficient.

B. Statement 2 ALONE is sufficient to answer the question, but statement 1 alone is NOT sufficient.

C. BOTH statements 1 and 2 TOGETHER are sufficient to answer the question, but NEITHER statement ALONE is sufficient.

D. Each statement ALONE is sufficient to answer the question.

E. Statement 1 and 2 TOGETHER are NOT sufficient to answer the question.

Consider statement (1): the product of xy is negative.

If x*y is negative, then x must be negative and y must be positive, or vice versa.

We know that x is less than y, so x must be negative. We also know that x and y are consecutive odd integers. Therefore, x must be -1 and y must be 1. Statement (1) is sufficient.

Statement (2): x+y is the square of an integer. Some possibilities that satisfy the requirements are:

x = -1, y = 1 (x+y = 0, 0 is the square of 0)

x = 1, y = 3 (x+y = 4)

x = 7, y = 9 (x+y = 16)

and so on and so forth. Statement (2) alone is not sufficient.

Answer = (A)

Q2. If x is an odd negative integer and y is an even integer, which of the following statements must be true?

I. (3x - 2y) is odd

II. xy^2 is an even negative integer

III. (y^2 - x) is an odd negative integer

A. I only

B. II only

C. I and II

D. I and III

E. II and III

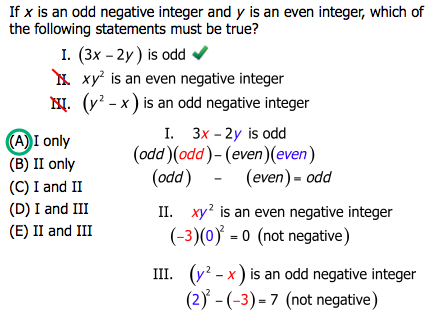
Answer = (A)

FAQ: Is zero an even integer?

A: It sure is! 0 is an even integer that is neither positive nor negative.

FAQ: When I plug in values for the 1st choice the answer is negative odd integer. The 1st choice only mentions that (3x - 2y) is odd. Can our answer be negative as well?

A: Absolutely! A negative odd integer is still odd. The first answer choice is only concerned with whether the result is odd or even. Whether it's positive or negative, doesn't actually matter for the 1st answer choice.