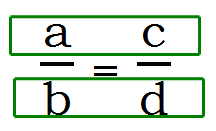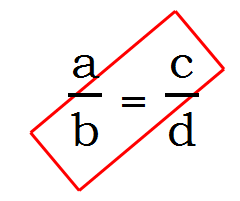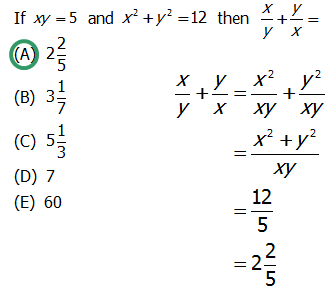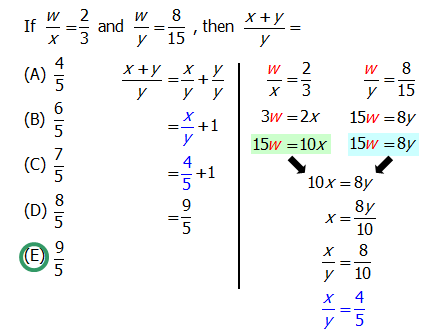Fractions is hard?
Why Fractions Are Hard
Of all the math topics that raise dread, fear, anxiety, and confusion, few do so as consistently and as potently as do fractions. I have my own personal theory why fractions are hard. The trouble is: think about when you learned fractions — maybe the third, fourth, and/or fifth grades. That's when fractions are usually taught, but there are two problems with that. First of all, that's before the tsunami of puberty hits you and virtually obliterated all previously held logical connections in your head. More importantly, fractions, like many other topics in math, involve sophisticated patterns, but in the fourth grade, no one is capable of abstraction, so instead you are just taught to reproduce patterns mechanically, and relying on mechanical repetition has severe limitations: similarly looking things become conflated, and when you get confused, you basically don't know what to do. Many people simply give up at that point.
The solution is re-approach those mechanical procedures, but with understanding. When you understand why you do each thing, then (a) you can remember it much better, and (b) in a moment of confusion you can figure out what to do. I will lead you through fractions from the ground up.
What is a Fraction?
A fraction is a way of showing division. The fraction \dfrac{2}{7} means the number you get when you divide 2 by 7. The top of a fraction is called the numerator, and the bottom of a fraction is called the denominator.
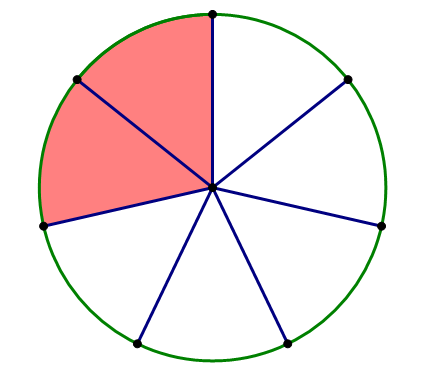
The fraction \dfrac{2}{7} also means the following. Imagine dividing something whole into seven equal parts — one of those parts is \dfrac{1}{7} of the whole, so \dfrac{2}{7} = 2*\bigg(\dfrac{1}{7}\bigg) is two of those parts. Probably this diagram will call up dim memories from your prepubescent mathematical experiences.
That, visually, represents \dfrac{2}{7}. Two vital things to remember about \dfrac{2}{7} — one is that \dfrac{2}{7} is two of the thing called \dfrac{1}{7} — that is, \dfrac{2}{7} = 2*\bigg(\dfrac{1}{7}\bigg), and second is this visual perspective that is always vital.
Notice that if you have the fractions \dfrac{4}{14} or \dfrac{10}{35}, they both cancel down to \dfrac{2}{7}. Cancelling is division. That's a big idea — thus, when you have \dfrac{4}{20}, and you cancel (i.e. divide) the 4's in the numerator and the denominator, they don't simply "go away" (a fourth-grade mechanical way of thinking), but rather what's left in the numerator is 4 \div 4 = 1, and we get \dfrac{4}{20} = \dfrac{1}{5}.
Adding and Subtracting Fractions
First of all, let's address the common mistake: when you add fractions, you can't simply add across in the numerator and denominator (this is the mistake people make when they mechanically perform the rule for multiplication with addition instead!)
\dfrac{a}{b} + \dfrac{c}{d} \not = \dfrac{a+c}{b+d}
You may dimly remember that you only can add and subtract fractions when you have a common denominator. That's true, but why is that true? Believe it or not, the basis of this fact is none other than the Distributive Law, a(b + c) = ab + ac. For example, if I add 3x and 5x, I get 3x + 5x = 8x — according to the Distributive Law, I can add two terms of the same thing, BUT if I want to add 3x + 5y, I can't simplify that any further and must keep it as 3x + 5y. If you add two terms of the same underlying thing, you can combine the terms, but if you are adding proverbial apples and oranges, you can't combine. Well, \dfrac{3}{11} + \dfrac{5}{11} is really just 3*\bigg(\dfrac{1}{11}\bigg) + 5*\bigg(\dfrac{1}{11}\bigg) — so, by the Distributive Law, you are allowed to add two terms of the same thing: \dfrac{3}{11} + \dfrac{5}{11} = \dfrac{8}{11}
When the denominators are not the same — \dfrac{3}{8} + \dfrac{1}{6} — then you can't add them as is, but you can take advantage of a sleek mathematical trick. We know that any number over itself, say \dfrac{3}{3}, equals 1, and you can always multiply by 1 and not change the value of something. Therefore, I could multiply \dfrac{3}{8} by some \dfrac{a}{a}, and multiply \dfrac{1}{6} by some other \dfrac{b}{b}, and both would retain the same value. I want to multiply each so that I find the Least Common Denominator (LCD), which here is 24. Thus
\bigg(\dfrac{3}{8}\bigg) + \bigg(\dfrac{1}{6}\bigg) = \bigg(\dfrac{3}{8}\bigg)*\bigg(\dfrac{3}{3}\bigg) + \bigg(\dfrac{1}{6}\bigg)*\bigg(\dfrac{4}{4}\bigg) = \bigg(\dfrac{9}{24}\bigg) + \bigg(\dfrac{4}{24}\bigg) = \bigg(\dfrac{13}{24}\bigg)
The same thing works for subtraction:
\bigg(\dfrac{3}{8}\bigg) - \bigg(\dfrac{1}{6}\bigg) = \bigg(\dfrac{3}{8}\bigg)*\bigg(\dfrac{3}{3}\bigg) - \bigg(\dfrac{1}{6}\bigg)*\bigg(\dfrac{4}{4}\bigg) = \bigg(\dfrac{9}{24}\bigg) - \bigg(\dfrac{4}{24}\bigg) = \bigg(\dfrac{5}{24}\bigg)
Multiplying Fractions
This is the easiest of all fractions rules. To multiply fractions, multiply across in the numerators and denominators.
\dfrac{5}{7} \times \dfrac{2}{3} = \dfrac{10}{21}
What's a little tricky about multiply is what you can cancel. If you are multiply two fractions, of course you can cancel any numerator with its own denominator, but you can also cancel one numerator with another denominator. Sometimes, that is called "cross-cancelling", which I think is a 100\% useless term that reinforces fourth-grade mechanical thinking. I think it's much more effective to remember: when you multiply fractions, you can cancel any numerator with any denominator. Here's a horrendous multiplication problem that simplifies elegantly with the liberal use of cancelling.
\dfrac{26}{48} \times \dfrac{18}{\red{56}} \times \dfrac{\red{64}}{39} = \dfrac{\red{26}}{48} \times \dfrac{18}{7} \times \dfrac{8}{\red{39}} = \dfrac{2}{\red{48}} \times \dfrac{18}{7} \times \dfrac{\red{8}}{3} = \dfrac{2}{\red{6}} \times \dfrac{\red{18}}{7} \times \dfrac{1}{\red{3}} = \dfrac{2}{1} \times \dfrac{\red{1}}{7} \times \dfrac{1}{1} = \green{\dfrac{2}{7}}
Dividing Fractions
First of all, multiplying by \dfrac{1}{3} is the same as dividing by 3. That's just the fundamental definition of fraction as division. This also means, dividing by \dfrac{1}{3} is the same as multiplying by 3. This pattern suggests, correctly, that dividing by a fraction simply means multiplying by its reciprocal:
\dfrac{5}{12} \div \dfrac{3}{8} = \dfrac{5}{\red{12}} \times \dfrac{\red{8}}{3} = \dfrac{5}{3} \times \dfrac{2}{3} = \dfrac{10}{9}
Notice, as always, cancel before you multiply. Dividing a fraction by a number follows the same pattern:
\dfrac{\bigg(\dfrac{6}{13}\bigg)}{3} = \dfrac{6}{13} \div \dfrac{3}{1} = \dfrac{6}{13} \times \dfrac{1}{3} = \dfrac{2}{13}
Notice, this is really the same idea as: dividing by 3 means the same thin as multiplying by \dfrac{1}{3}. Also, again, notice we cancel before we multiply.
Proportions
Another word for a fraction is a ratio: ratios and fractions are exactly the same thing. A proportion is when you have two ratios, two fractions, set equal to each other. For example,
\dfrac{x}{12} = \dfrac{33}{28}
One legitimate move is to cross-multiply, although doing so here would violate the ultra-strategic dictum: cancel before you multiply. And it's precisely this issue, what can you cancel and what can't cancel in a proportion, that causes endless confusion. Let's look at the general proportion \dfrac{a}{b} = \dfrac{c}{d}.
First of all, as always, you can cancel any numerator with its own denominator — you can cancel common factors in a \And b, or in c \And d. Furthermore, a proportion, by its very nature, is an equation, and you can always multiply or divide both sides of an equation by the same thing. This means: you can cancel common factors in both numerators (a \And c) or in both denominators (b \And d). The following diagrams summarize all the legitimate directions of cancellation in a proportion.
The following are highly tempting but complete illegal ways to cancel in proportions:
The trouble is, folks mechanically memorize the cancelling pattern for multiplying fractions — or even worse, they learn an utterly useless term like "cross-cancelling" — and then they mechanically apply that pattern when there's an equal sign between the two fractions instead of a multiplication sign. This is a major mistake, and any time a proportion appears on the QUANT, the test-maker is expecting a large flock of test-takers to fall into this trap.
Let's solve the proportion we wrote above, with proper cancelling:
\dfrac{x}{\red{12}} = \dfrac{33}{\red{28}} \implies \dfrac{x}{3} = \dfrac{33}{7} \implies x = \dfrac{99}{7}
Notice, in that last step, to isolate x, all we had to do was multiply both sides by 3. Cross-multiplying, while always legal in a proportion, often is a waste of time that simply adds extra steps.
Practice Questions
I hope this refresher has clear up some fractions concepts for you. The best way to cement a new mathematical understand: practice, practice, practice!
Q1. If xy = 5 and x^2 + y^2 = 12, then \dfrac{x}{y} + \dfrac{y}{x} =
A. 2\dfrac{2}{5}
B. 3\dfrac{1}{7}
C. 5\dfrac{1}{3}
D. 7
E. 60
We're asked to find the value of:
\dfrac{x}{y} + \dfrac{y}{x}
Let's first combine these two fractions into one. We can obtain a common denominator of xy if we multiply the left fraction by \dfrac{x}{x} and the right fraction by \dfrac{y}{y}:
\dfrac{x^2}{xy} + \dfrac{y^2}{xy} = \dfrac{x^2 + y^2}{xy}
From here, we can substitute in the values from the prompt that x^2 + y^2 = 12, and that xy = 5:
\dfrac{12}{5}
And now, we convert the above into a mixed fraction:
2 \dfrac{2}{5}
Answer = A
Q2. If \dfrac{w}{x} = \dfrac{2}{3} and \dfrac{w}{y} = \dfrac{8}{15}, then \dfrac{(x + y)}{y} =
A. \dfrac{4}{5}
B. \dfrac{6}{5}
C. \dfrac{7}{5}
D. \dfrac{8}{5}
E. \dfrac{9}{5}
Answer = E
Q3. To reach her destination, Jeanette must drive 90 miles. If she drives 5 miles every 7 minutes, how much time will it take her to reach her destination?
A. 2 hours and 2 minutes
B. 2 hours and 6 minutes
C. 2 hours and 10 minutes
D. 2 hours and 12 minutes
E. 2 hours and 15 minutes
Answer = B