The Area of an Equilateral Triangle

Suppose you have an equilateral triangle with sides of length s. We know all the sides have the same length. It’s not relevant for finding the area, but we also know that all three angles equal 60 degrees.

Step #1: We know that the formula for the area of a triangle is A=\dfrac{1}{2}*bh. The base is clearly s, but we need a height.

Step #2: We draw an altitude, that is, a line from B that is perpendicular to AC. The length of this line is the height needed in A = \dfrac{1}{2}*bh.

Step #3: Point D is the midpoint of AC, so AD = \dfrac{s}{2}. Also, \angle ADB is 90 \degree.

Step #4: Call the length of BD h, and apply the Pythagorean Theorem in \triangle ADB:

{\Big(\dfrac{s}{2}\Big)}^2+h^2=s^2

\dfrac{s^2}{4}+h^2=s^2

h^2=s^2-\dfrac{s^2}{4}

h^2=\dfrac{4s^2}{4}-\dfrac{s^2}{4}

h^2=\dfrac{3s^2}{4}

h=\dfrac{s*\sqrt{3}}{2}

Step #5: Now that we have the height in terms of s, we can find the area.

Area=\dfrac{1}{2}*bh

Area=\dfrac{\dfrac{1}{2}*s*(s*\sqrt{3})}{2}

Area=\dfrac{{s^2}\sqrt{3}}{4}

That last formula is, indeed, the area of an equilateral triangle, and remembering it will be a definite time-saver on Math. Again, I don’t want you to memorize it. Rather, I strongly encourage you to remember this five step argument: practice recreating it step-by-step until you can flawlessly recapitulate the entire thing by yourself. Then, you won’t merely remember this formula — you will own it!

I encourage you to do that with each important math formula. If you don’t know the steps that lead to a particular formula, and can find it online, leave me a comment :).

Q1. If the length of each side of an equilateral triangle were increased by 50 percent, what would be the percent increase in the area?

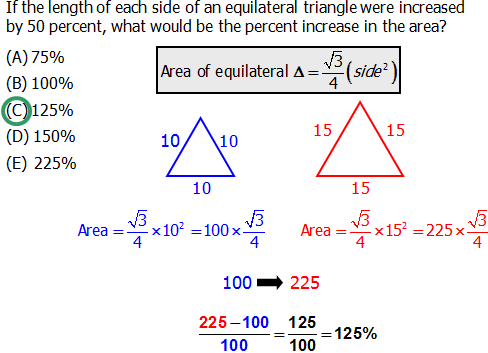
Answer = C