GRE Quantitative Comparison Tip #4 – Comparing in Parts

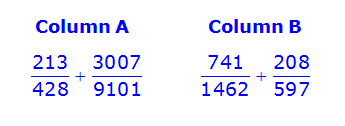
To set up today's Quantitative Comparison (QC) strategy, please solve the following question:

A. The quantity in Column A is greater

B. The quantity in Column B is greater

C. The two quantities are equal

D. The relationship cannot be determined from the information given

There are several different ways to solve this question. For example, we could add the fractions in each column, and then rewrite both sums with a common denominator and then compare them (yikes!). Or, we could use the onscreen calculator to convert each fraction to a decimal and find the sum in each column (yeesh!).

Both of these approaches would take a long time.

Fortunately, we already know that, since the test-makers are reasonable, there MUST be an easier way to solve this question (please read my previous post: The Reasonable Test-Maker).

The fastest way to solve this question is to estimate and compare the columns in parts.

Here's how it works.

First notice that \dfrac{213}{428} is approximately \dfrac{1}{2}. Now, for this question, we need to be a little more accurate than that. Notice that, since \dfrac{214}{428} = \dfrac{1}{2}, it must be the case that \dfrac{213}{428} is a little bit less than \dfrac{1}{2}, which we'll denote as \bigg(\dfrac{1}{2}\bigg)^{-}.

Using similar logic, we can see that, since \dfrac{3007}{9021} = \dfrac{1}{3}, it must be the case that \dfrac{3007}{9101} is a little bit less than \dfrac{1}{3}, which we'll denote as \bigg(\dfrac{1}{3}\bigg)^{-}.

Next, since \dfrac{731}{1462} = \dfrac{1}{2}, it must be the case that \dfrac{741}{428} is a little bit more than \dfrac{1}{2}, which we'll denote as \bigg(\dfrac{1}{2}\bigg){+}.

Using the same logic, we can see that \dfrac{208}{597} is a little bit more than \dfrac{1}{3}, which we'll denote as \bigg(\dfrac{1}{3}\bigg)^{+}.

At this point, we can simplify the two columns as:

From here, we can compare the two sums in parts.

Since \bigg(\dfrac{1}{2}\bigg)^{+} is greater than \bigg(\dfrac{1}{2}\bigg)^{-}, and since \bigg(\dfrac{1}{3}\bigg)^{+} is greater than \bigg(\dfrac{1}{3}\bigg)^{-}, the sum of \bigg(\dfrac{1}{2}\bigg)^{+} and \bigg(\dfrac{1}{3}\bigg)^{+} must be greater than the sum of \bigg(\dfrac{1}{2}\bigg)^{-} and \bigg(\dfrac{1}{3}\bigg)^{-}.

As such, the answer must be B.