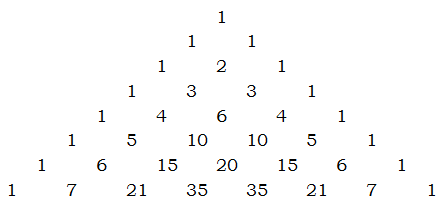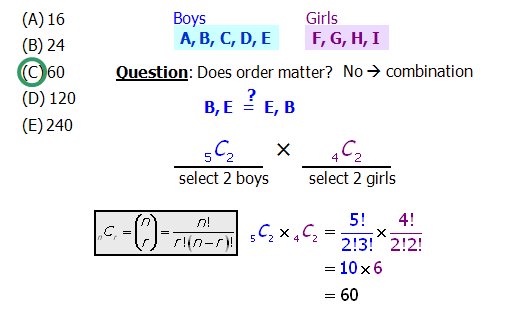QUANT: Calculating Combinations
First, a few practice questions. Remember — no calculator!
Q1. A radio station has to choose three days of the seven in a week to broadcast a certain program, and that set will repeat each week. The program can be broadcast equally on any of the seven weekdays — weekdays vs. weekends don't matter at all — nor does it matter whether the days the program airs are adjacent or not. Absolutely any three of the seven weekdays can be chosen. How many different three-day combinations of the seven weekdays can be constructed?
(A) 9
(B) 15
(C) 21
(D) 35
(E) 56
Q2. Claudia can choose any two of four different candles and any 8 of 9 different flowers for a centerpiece arrangement. Given these choices, how many candle + flower groupings can she select?
(A) 54
(B) 72
(C) 96
(D) 144
(E) 432
Q3. A newly-wed couple is using a website to design an eBook Wedding Album to distribute to their friends and families. The template they have chosen has places for 3 large photos and 19 smaller photos. The couple has 6 large photos they could use for those three slots, and 21 smaller photos they could use for those 19 slots. Given these choices, how many different possible albums could they create?
(A) 3,150
(B) 4,200
(C) 5,040
(D) 20,520
(E) 84,000
Q4. From a total of 5 boys and 4 girls, how many 4-person committees can be selected if the committee must have exactly 2 boys and 2 girls?
(A) 16
(B) 24
(C) 60
(D) 120
(E) 240
In this post, we'll discuss how to handle questions like this — without a calculator.
Combinations
Mathematically, a combination is a group of things, irrespective of order. For example, {A, B, D} and {D, A, B} and {B, A, D} are all the same combination — order doesn't matter at all. The expression \bold{{\Large{C}}_n^r} (read "n \space choose \space r") is the expression for the number of combinations of r things, r choices, you can make from a pool of n unique items. For example,
\bold{{\Large{C}}_6^3} = the number of combinations of three one can choose from a pool of six unique items.
In a previous post about combinations, I give the following formula for {C}_n^r
\bold{{\Large{C}}_n^r} = \dfrac{n!}{r!(n-r)!}
where the exclamation point ("!") is the factorial symbol — n! means the product of all the positive integers from n down to 1. Using this formula, we could compute the value of {C}_6^3 =
\bold{{\Large{C}}_6^3} = \dfrac{6!}{3!*(6-3)!} = \dfrac{6!}{3!*3!} = \dfrac{6*5*4*\red{\cancel{3*2*1}}}{(3*2*1)*\red{\cancel{(3*2*1)}}} = \dfrac{\red{\cancel{6}}*5*4}{\red{\cancel{6}}} = 5*4 = 20
So, it turns out, there are twenty ways to pick a set of three items from a pool of six unique items. That's one way to calculate nCr, but it's not the only way.
Pascal's Triangle
The mathematician and philosopher Blaise Pascal (1623 – 1662) created a magical triangular array of numbers known now as Pascal's Triangle:
How does this pattern work? Well, of course, the edges are diagonals of 1's. Every inside number is the sum of the two numbers above it in the previous row, diagonally to the left and diagonally to the right. For example, the 2 is the sum 1+1; both 3's are the sum 1+2; both 4's are the sums 1+3; the 6 is the sum 3+3, etc. They often show Pascal's Triangle to grade school students to give them practice with addition.
Despite its relatively easy origins, Pascal's Triangle is a treasure trove of miraculous mathematical properties. Most relevant for us right now is: Pascal's Triangle is, among other things, an array of all possible \bold{{\Large{C}}_n^r}'s.
\bold{{\Large{C}}_n^r} = the r^{th} entry of the nth row of Pascal's Triangle
In that definition, we have to be careful — we have to start counting at zero instead of one. The top 1 on Pascal's Triangle is the zeroth row, zeroth entry, \bold{{\Large{C}}_0^0} = 1 (a relatively meaningless number in terms of combinations!) The next row (1, 1) is the first row, and the next row is the second row (1, 2, 1), etc. Notice that the second number in any row (as well as the penultimate number in any row) equals the row number. The first number (always 1) is actually the zeroth entry, so that second number would actually be the first entry — the first entry of the nth row always equals n. In other words
\bold{{\Large{C}}_n^1} = n
That makes sense: if we have n different items, we have exactly n ways of selecting any one item. Those entries, the first entries of each row, line along a diagonal down the left side of the triangle. Because of the complete symmetry of the triangle, this always equals the numbers on the corresponding diagonals on the right side, which would be the (n-1) entries of each row. Thus:
\bold{{\Large{C}}_n^1} = \bold{{\Large{C}}_n^{n-1}} = n
When you have to figure out \bold{{\Large{C}}_n^r} when n \And r are both relatively small numbers, it may be easier simply to jot down the first few rows of Pascal's Triangle. For example, with what we have showing, we can see that \bold{{\Large{C}}_6^3}, the 3^{rd} entry of the 6^{th} row, is 20 — the same as the answer we found via the factorials formula.
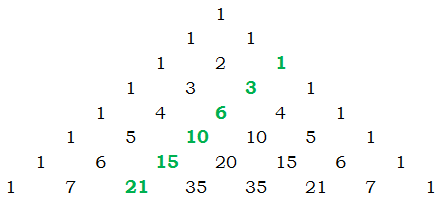
Things get even more interesting when we move to the next diagonal in, shown in green here:
These numbers, the set of the second entries in each row, are the triangular numbers. Among other things, the second entry in the n row is the sum of the first n-1 positive integers. For example
3 = 2 + 1
6 = 3 + 2 + 1
10 = 4 + 3 + 2 + 1 etc.
The formula for this is:
\bold{{\Large{C}}_n^2} = \dfrac{n(n-1)}{2}
Because we have a formula, we can calculate this for much higher numbers. For \bold{{\Large{C}}_{21}^2}, we would have to write out everything to the twenty-first row of Pascal's Triangle, an arduous undertaking. Rather, we could simply use the formula
\bold{{\Large{C}}_{21}^2} = \dfrac{21(20)}{2} = 21*10 = 210
Notice that the symmetry of Pascal's Triangle also provides tremendous insight into the nature of the nCr numbers. First of all, in any row, the second entry, the triangular number in that row, must be equal to the third-to-last entry of the row, that is, the (n-2) entry of the row. Thus
\bold{{\Large{C}}_n^2} = \bold{{\Large{C}}_n^{n-2}} = \dfrac{n(n-1)}{2}
Thus, via the triangular numbers, we have a formula, not only for the second entry of each row, but also for the third-to-last entry of every row. Thus, it's very easy to figure out the first three or last three numbers in any row. More generally, symmetry guarantees that:
\bold{{\Large{C}}_n^r} = \bold{{\Large{C}}_n^{n-r}}
If you think about combinations this makes sense: if we have a pool of n unique items, then every time we choose a unique set of r items, we necessarily exclude a corresponding unique set of (n-r) items. In other words, there is necessarily a 1-to-1 correspondence between unique sets of r elements and unique sets of the other (n-r) elements — because there's a 1-to-1 correspondence, the number of each must always be the same. This is precisely what that equation says.
Practice question explanations
Q1. Behind the story, we are really being asked to evaluate \bold{{\Large{C}}_7^3}. We could use the factorial formula, but above we conveniently happen to have Pascal's Triangle written out to the seventh row. We see that \bold{{\Large{C}}_7^3}, the third entry of the seventh row, is 35.
Answer = D
Q2. For this one, we have to use the Fundamental Counting Principle (FCP) as well as information about combinations. For the flowers, we want \bold{{\Large{C}}_9^8}, which by the symmetry of Pascal's Triangle, has to equal \bold{{\Large{C}}_9^1}, the first entry in the row, which of course equals the row number.
\bold{{\Large{C}}_9^8} = \bold{{\Large{C}}_9^1} = 9
That's the number of flower combinations. For the candles, \bold{{\Large{C}}_4^2}, we read the second entry of the fourth row of Pascal's Triangle.
\bold{{\Large{C}}_4^2} = 6
Now, by the FCP, we multiply these for the total number of centerpiece arrangements: 6*9 = 54.
Answer = A
Q3. For the large photos, we need \bold{{\Large{C}}_6^3}, which we calculated in the article:
\bold{{\Large{C}}_6^3} = 20
For the smaller photos, we need \bold{{\Large{C}}_{21}^{19}}, which by symmetry must equal \bold{{\Large{C}}_{21}^{2}}, and we have a formula for that. In fact, in the article above, we already calculated that \bold{{\Large{C}}_{21}^{2}} = 210.
Now, by the FCP, we just multiply these: total number of possible albums = 20*210 = 4200.
Answer = B
Q4. From a total of 5 boys and 4 girls, how many 4-person committees can be selected if the committee must have exactly 2 boys and 2 girls?
FAQ: Why do we multiply the two values? Why not add \bold{{\Large{C}}_5^2} and \bold{{\Large{C}}_4^2}?
A:
In a way, this is just a question of "and" or "or." Make sure that we don't confuse it with probability, though, which has very different rules for "and" and "or."
In this question, we're looking for the number of different ways we can choose both 2 boys and 2 girls. In the end, we're really choosing people to go in one group — we're not considering the two boys as a separate group from the 2 girls.
Here's a couple of simple examples to illustrate what I mean by this:
If I have an a peach, a plum, an apricot, an orange, a lime, and a lemon, how many ways can I pick two pieces of fruit with pits OR two pieces of citrus fruit? Well, there are \bold{{\Large{C}}_3^2} possible groups of stone fruit and \bold{{\Large{C}}_3^2} possible groups of citrus fruit. That's 3 + 3 = 6.
- peach, plum
- peach, apricot
- plum, apricot
- orange, lemon
- orange, lime
- lemon, lime
From that same group, how many ways can I pick two pieces of fruit with pits AND two pieces of citrus fruit? This gives more possibilities.
- peach, plum, orange, lemon
- peach, plum, orange, lime
- peach, plum, lemon, lime
- peach, apricot, orange, lemon
- peach, apricot, orange, lime
- peach, apricot, lemon, lime
- plum, apricot, orange, lemon
- plum, apricot, orange, lime
- plum, apricot, lemon, lime
That makes 3 * 3 = 9 possible groups.
Really, we found that there are 3 ways to choose 2 stone fruits and 3 ways to choose two citrus fruits. If we're we're counting the possibilities of both together in one group, then we have to multiply the results, as per the fundamental counting principal (in the related lessons below).
This is the same as the boys and girls situation. If we asked how many ways you can make a group of 2 boys or a group of 2 girls, then we would add the two. But since we're combining these into one group, we're looking at boys and girls, and so we multiply.
Answer = C